Это вторая часть статьи посвященной расширенному нелинейному анализу с упором на закритическое поведение объекта. Если вы не читали первую часть статьи о расширенном нелинейном анализе закритического поведения в Femap: Advanced Nonlinear Solver, то ознакомиться ней можно по ссылке.
Ранее мы уже говорили о поведении при потере устойчивости на примере тонкостенного цилиндра. Данное руководство посвящено нелинейному анализу коробчатой балки. Следующая демонстрация расширенного нелинейного анализа в Femap: Advanced Nonlinear Solver будет проводиться на примере коробчатой рамы крыловидной конструкции.

На рисунках показана внешняя сторона, а внутри можно увидеть ребра, лонжероны в кормовой и носовой части, и продольные балки. Если обратить внимание на толщины, то видно, что внутренняя сторона обладает гораздо большей жесткостью, чем наружная.

Передняя часть крыла сильнее укреплена продольными балками, чем задняя, в которой продольных балок нет вообще. Стоит отметить один момент, касающийся этой модели – она полностью сделана из алюминия.
Проверка модели
В этой КЭ-модели была применена нелинейная модель материала. Мы обнаружили, что нелинейная модель материала «Plastic» точнее аппроксимирует поведение нелинейности работы материалов при проведении расширенного нелинейного анализа в Femap: Advanced Nonlinear Solver.

Если Вы собираетесь работать с нелинейной пластичностью, Вам следует сначала обратить внимание на следующие моменты:
- Вам необходимо выбрать подходящий критерий пластичности (yield criteria) и задать предел текучести материала (yield stress). В данной задаче мы используем критерий фон Мизеса (von Mises)
- Вам необходимо создать кривую деформирования материала в виде функции.

Кривая деформирования материала
В зоне упругой деформации мы дошли до напряжений 65 KSI (тысяч фунтов на кв. дюйм), а в зоне пластики мы ушли намного дальше.


Если Вы собираетесь работать с нелинейным пластичным материалом, то Вам необходимо определить кривую деформирования материала на максимальном диапазоне деформаций. Постарайтесь убедиться в том, что Ваша модель не выходил за пределы кривой зависимости деформаций от напряжений.
Результат
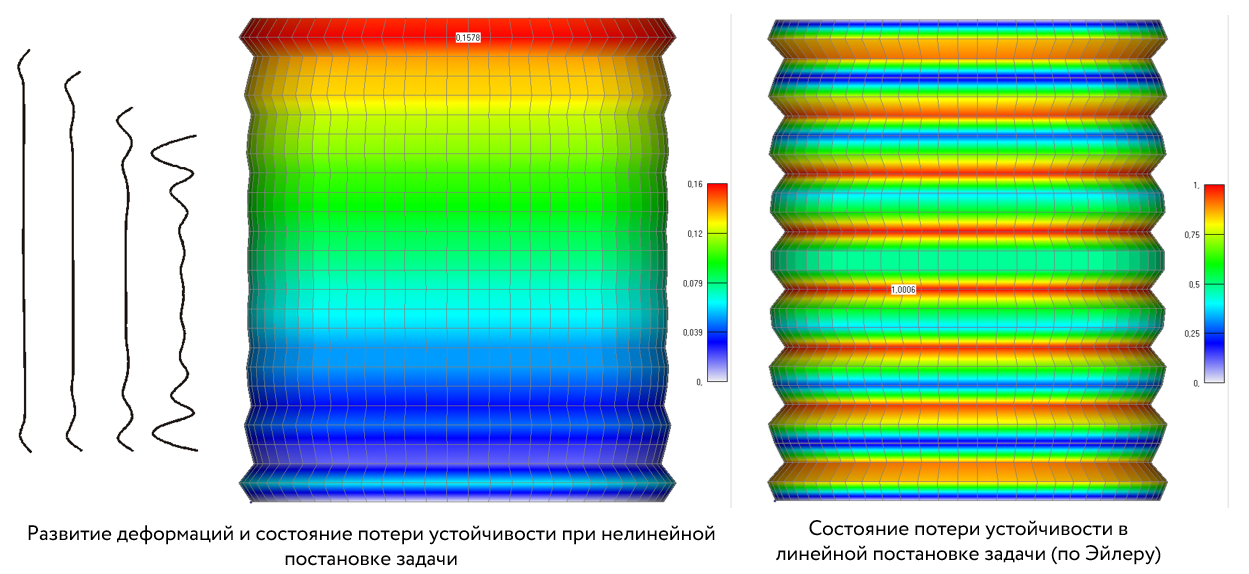
Теперь мы готовы выйти на финишную прямую. Как можно заметить, появилась потеря устойчивости обшивки в некоторых местах крыла. Взглянув на заднюю сторону, Вы увидите, что не только обшивка была деформирована и сбросила нагрузку, а изменения начались и в других частях конструкции.

На задней части можно увидеть неровности на сетке и пластическое напряжение в этой зоне увеличилось на 50% (что, скорее всего, приведет к полной потере устойчивости).

Спереди же мы можем наблюдать колебания продольных балок. Эти колебания выходят за пределы движения в одной плоскости что, скорее всего, приведет к разгрузке.

Далее, давайте начнем с более раннего временного периода и посмотрим, что произойдет, когда мы будем наращивать нагрузку.

Как мы видим, все больше и больше конструктивных элементов обшивки будет терять устойчивость, и в конечном итоге все большая часть нагрузки будет восприниматься лонжероном. В нелинейном анализе хорошо то, что, даже учитывая всю потерю устойчивости и нелинейность в модели, мы все еще можем получить сходимость и посмотреть,
что произойдет с запланированным и незапланированным напряжениями.
Управление анализом (Analysis Manager)
Когда Вы работаете в режиме нелинейного анализа, окно управления анализом появляется во всплывающем меню.

На этом графике Вы увидите, сколько потребуется вашему решению, чтобы произошла сходимость анализа. Это не прямая линия, квадратом выделено место, где модель испытывает трудности со сходимостью. Если вспомнить нашу модель, между временными шагами 20 и 30 начала формироваться потеря устойчивости обшивки. Вы можете использовать это, чтобы устранить неисправность и выяснить, где Вы хотите добавить несколько временных шагов или изменить параметры сходимости,
чтобы помочь решателю добиться сходимости анализа.
Заключение
Расширенный нелинейный анализ в Femap: Advanced Nonlinear Solver может быть использован в целях получения более реалистичного поведения конструкции, когда существуют геометрические или физические нелинейности. Он может уловить нелинейную потерю устойчивости и помочь определить наилучшие конструктивные решения для дальнейшего исследования закритического поведения.





.svg)






























.jpg)
.jpg)



