Femap. Нелинейный статический анализ

Введение в нелинейный анализ

В зависимости от условий нагружения поведение большинства конструкций на практике является нелинейным. Во многих ситуациях допустимо рассматривать линейное поведение в предположении малых перемещений и деформаций. В других случаях для получения корректных результатов необходимо учитывать нелинейное поведение конструкций.

Поведение конструкции можно считать нелинейным в тех случаях, когда нагрузки, свойства материалов, условия контактного взаимодействия или жесткость системы являются функциями перемещения. При больших перемещениях и поворотах предположение о линейном соотношении деформация–перемещение, которое используется для линейного анализа, является неверным.

Нелинейность можно разделить на три типа:

• геометрическая нелинейность, когда в результате деформирования тел происходит сильное изменение жесткостных свойств или нагрузок;
• физическая нелинейность, то есть необходимость учета нелинейных свойств материалов;
• нелинейность граничных условий, а именно контактное взаимодействие поверхностей тел.

По сравнению с линейным анализом, нелинейный требует больших вычислительных ресурсов и большей квалификации от инженера. Поскольку используется единая для линейного и нелинейного анализов библиотека конечных элементов, то пользователь может осуществить быстрый переход от линейной задачи к нелинейной и наоборот.

Нелинейные решения NX NASTRAN

• NLSTATICSOL 106 (нелинейный статический);
• NLTRANSOL 129 (нелинейный динамический);
• NLSCHSOL159 (нестационарный нелинейный тепловой);
• ADVNLSOL601, 106 (расширенный нелинейный статический);
• ADVNLSOL601, 129 (расширенный нелинейный динамический, неявный);
• ADVNLSOL701 (расширенный нелинейный динамический, явный).
  ‍

‍

При решении задач с учетом различного рода нелинейностей для решений SOL 106/129, ADVNL 601,106/129 поддерживаются все виды элементов, используемые для линейного анализа, с небольшими изменениями в их формулировках.

Для явного решения ADVNL 701 существуют следующие ограничения на использование КЭ элементов:

• не поддерживаются плоско-напряженные и плоско-деформируемые 2D элементы;
• не поддерживаются многослойные оболочки с физическими свойствами PCOMP;
• не поддерживаются осесимметричные элементы;
• из оболочечных элементов поддерживаются только CQUAD4, CTRIA3;
• из 3D элементов поддерживаются только CHEXA8, CPENTA6, CTETRA4.

Использование нелинейных решений NX Nastran позволяет применять любые ограничения на степени свободы и почти все виды нагрузок, за исключением:

• углового центробежного ускорения;
• предварительного затяга болтов в ADVNL 701;
• условия склеивания в ADVNL 701.

Из-за особенности методов решения нелинейных задач рекомендуется прикладывать нагрузку постепенно (в несколько шагов или подшагов).

• Для этого в статическом анализе решения NLSTATIC 106 нагрузка задается в виде постоянной величины, и указывается шаг ее приращения.
• Для статического анализа в решении ADVNL 601,106 нагрузка может быть как постоянной (не зависимой от времени), так и зависимой от времени для ее пошагового приложения с целью улучшения сходимости нелинейного решения. В этом случае время играет роль фиктивной величины для изменения нагрузки.
• Исключение составляет учет ползучести материала в статическом анализе, так как свойства материала при ползучести зависят от времени.

Выполнение нелинейного анализа может сопровождаться различными комбинациями типов нелинейностей, наиболее распространенный случай – это учет упругопластических свойств материала, больших перемещений и контактного взаимодействия. По умолчанию используются малые перемещения и деформации.

• Параметр PARAM, LGDISP, 1 определяет учет больших перемещений, PARAM, LGSTRN, 1 определяет учет больших деформаций, при этом учет больших деформаций автоматически подразумевает и учет больших перемещений.
  ‍

Геометрическая нелинейность

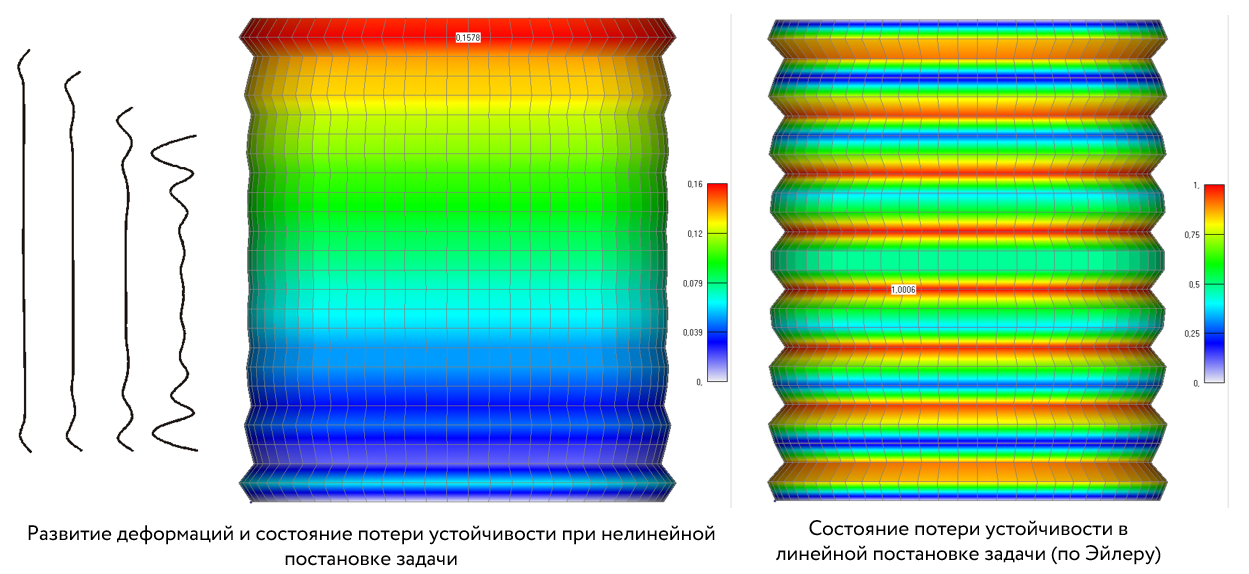
Часто возникает необходимость учитывать эффект геометрической нелинейности во время моделирования поведения конструкции при возникновении больших перемещений, больших деформаций, учета следящей нагрузки и поведения конструкции после потери устойчивости.

• Учет геометрической нелинейности важен, например, для анализа устойчивости тонких пластин, вращения валов, формовки металла и т. д.
• В других случаях решение об учете геометрической нелинейности принимается исходя из опыта инженера. Таким образом, если прогиб пластины превышает 20% от ее толщины или прогиб балки превышает 2% от ее длины, то обычно учитывают геометрическую нелинейность.

На рисунке 1 изображены результаты статического линейного анализа (sol101) тонкой пластины в масштабе 1:1.

На рисунке 2 изображены результаты нелинейного анализа с учетом геометрической нелинейности (sol106). В линейном анализе нагрузка не меняет свое направление, в отличии от нелинейного – это видно по реакциям в закреплении на ребрах пластины.

Использование линейного анализа – это допущение, которое необходимо использовать разумно. Если у Вас получается большая разница результатов между линейным и нелинейным анализами, значит решать задачу в линейной постановке нельзя.

‍

Нелинейность материалов

При определенных условиях нагружения конструкции необходимо рассматривать нелинейные свойства материалов, например при использовании гиперупругих материалов или для учета упругопластических свойств металлов. Нелинейное поведение материала достаточно сложное, поэтому в зависимости от анализа и ситуации используют известные модели материалов, служащие для описания нелинейных эффектов, наиболее близких к реальности.

• Типы нелинейных материалов:
• гиперупругий;
• упругопластический;
• вязкоупругий;
• температурно-зависимый.
  ‍

Упругопластический материал

• При использовании линейного статического анализа предполагается, что напряжения линейно пропорциональны деформациям.
• Для установления линейной зависимости между напряжениями и деформациями используется модуль Юнга (Youngs Modulus).
• Если напряжения в конструкции превышают предел текучести, то обычно рассматривают материал с учетом его пластических свойств.

Пластичностью называется свойство тела сохранять деформированное состояние после прекращения действия нагрузки полностью или частично.

• Нелинейный анализ всех в NX Nastran позволяет учитывать нелинейную зависимость напряжений от деформаций и вычислять остаточные пластические деформации, возникающие в конструкции после снятия нагрузки.

NX Nastran поддерживает следующие критерии пластичности:

• Мизеса (von Mises) – для пластичного материала используется в большинстве случаев;
• Треска (Tresca) – для хрупких и некоторых пластичных материалов;
• Друкера-Прагера (Drucker-Prager) – для материалов типа грунта и бетона с внутренним трением;
• Мора-Кулона (Mohr-Coulomb) – для материалов типа камень с внутренним трением

NX Nastran позволяет задавать диаграмму деформирования материала одним из двух способов:

• В виде билинейной кривой, которая определяется значением начального напряжения пластичности (LIMIT1) и тангенсом угла наклона (H) прямой пластического участка;
• В виде кусочно-линейной зависимости, которая определяется табличными значениями напряжение–деформация, где первый участок соответствует упругому деформированию.

При возникновении пластических деформаций поверхность пластичности материала изменяется с ростом деформаций. Это явление называется упрочнением материала (Strain Hardening).

После того как материал испытал воздействие осевого усилия одного знака (например, растяжение) в области пластических деформаций, сопротивляемость этого материала пластической деформации при действии сил другого знака (сжатие) понижается. Это явление носит название эффекта Баушингера.

В NX Nastran существуют три модели упрочнения:

• Изотропное упрочнение (isotropic hardening), при котором точка пластичности при сжатии равна пластическим напряжениям растяжения;
• Кинематическое упрочнение (kinematic hardening), при котором величина упругого разгружения равна удвоенной величине начального напряжения пластичности. В этом случае эффект Баушингера отсутствует;
• Смешанное упрочнение (combined hardening) соответствует поведению материала между кинематическим и изотропным упрочнением.

Задание пластических свойств

Задание пластических свойств материала в табличном виде имеет следующие правила:

• Первая точка должна быть (0, 0);
• Должны быть заданы начальное напряжение пластичности (LIMIT1) и модуль Юнга;
• Вторая точка должна соответствовать введенному значению LIMIT1;
• Угол наклона линии, соединяющей первую и вторую точки, должен быть равен модулю Юнга;
• Остальные точки вводятся в терминах эффективных пластических деформаций;
• Последняя точка соответствует точке разрушения, использование параметра XTCURVE=0 позволяет «удалять» элементы, деформации в которых превышают значение в точке разрушения. Параметр DTDELAY контролирует задержку «удаления» этих элементов с целью улучшения сходимости решения.

Анализ остаточных деформаций рессоры

• Напряжения в рессоре шасси при нагружении предельными нагрузками превышают предел текучести материала
• Требуется определить остаточный прогиб рессоры после снятия нагрузки
• Из-за того, что результирующая нагрузка направлена под острым углом к оси рессоры, задача является геометрически нелинейной

• Повернем рабочую плоскость на угол 41 вокруг оси X, чтобы нормаль к плоскости была направлена в сторону колеса. Участки рессоры создаем командой Geometry Solid Primitives. Первый участок создаем длиной 180 мм. Выберем в диалоговом окне Solid Primitives (Твердотельные примитивы) опцию Direction: Positive (положительное направление), опцию Primitive: Cone (Конус), и зададим размеры Bot Radius (Нижний радиус)=16, Top Radius (Верхний радиус)=30, Height (Высота)=180.
• Передвинем рабочую плоскость: (F2); <Offset Distance>; Z Offset=180; <OK>. Повторим команду создания примитива, и создадим конус высотой 20 мм, нижним радиусом 30 и верхним радиусом 30.5 мм. Передвинем рабочую плоскость на 20 мм и создадим цилиндр высотой 180 мм и радиусом основания 30.5 мм. Передвинем рабочую плоскость на 180 мм и создадим конус высотой 720 мм и радиусами основания и вершины 30.5 мм и 17.5 мм соответственно.
• Используя команду Mesh Control Size on Solid, зададим размер элемента  равным 8, вид сетки (Hex Solid). Затем командой Mesh Control Size Along Curve  установим число разбиений образующих рессоры 4, 1, 4, 13, начиная с верхнего конца.

• Создадим нелинейный материал командой Model Material: Title=vt–22, Young_Modulus,_E=110000, Poisson_Ratio,_nu=0.3; <Nonlinear>; Plastic–Elastic=Yes, Plasticity Modulus, H=3700, Initial Yield Stress=900; <OK>; <OK>.
• Создадим командой Model Property свойство для объемных элементов, в котором укажем созданный материал.
• Выполним разбиение твердого тела на шестигранные элементы с помощью команды Mesh Geometry HexMeshSolid

‍

• Передвинем рабочую плоскость: (F2); <Offset Distance>; Z Offset=–380; <OK>.
• Создадим командой Model Coord Sys систему координат рессоры “RS_spring”, ориентированную по рабочей плоскости. Ось Z этой системы координат будет совпадать с осью рессоры.
• С помощью команды Model Constraint Node создадим граничные условия. Закрепим два узла в сечении рессоры 180 мм, по направлениям TX и TY, и два узлы на верхнем торце рессоры по направлениям  TX, TY и TZ.
• Создадим узел в точке A,  лежащей в плоскости колеса. Мы предполагаем, что при нагружении рессоры этот узел будет иметь большие перемещения, поэтому применять RBE для передачи нагрузки из точки A на рессору нельзя. Для этой цели используем элементы Rod большой жесткости, которыми соединим узел A с узлами нижнего торца рессоры.
• Создадим командой Model Property свойство «rod» для элементов Rod, в котором укажем материал vt–22 и площадь сечения стержня 1000 мм2. Создадим стержни с помощью команды Mesh Connection Closed Link. В первое множество включим узлы нижнего торца рессоры, во второе множество – узел в точке A. В диалоговом окне Generate Connection Options (опции генерации связей) вы-берем опцию Line Elements (линейные элементы) и в списке Property выберем свойство rod.
• Создадим два нелинейных варианта нагружения.
• В первом варианте «load» приложим в узле точки A заданную нагрузку по оси Y глобальной системы координат.
• Во втором варианте «unload» приложим в узле точки A формальную нагрузку равную 1.0.
• Для обоих вариантов зададим параметры нелинейного нагружения, выполнив команду Model Load Nonlinear Analysis. В диалоговом окне команды нажмем кнопку Default (по умолчанию). В поле Number of Incremental (число шагов нагружения) укажем 10, в списке секции Output Control (управление выводом) выберем 3..ALL для того, чтобы получить наборы векторов результатов на каждом шаге нагружения

• Создадим вариант нелинейного анализа с помощью команды Model Analysis. Выберем в списке Analysis Type (Тип анализа) {10..Nonlinear Static}. В секции Master Requests and Conditions Nonlinear Options включим опцию Use Load Set Options (Использовать параметры варианта нагрузок). Создадим два случая нагружения (Case) с помощью кнопки <MultiSet>. В отличие от линейного статического решения (1..Static) при котором для каждого случая вычисляется независимое решение, при нелинейном анализе заданные случаи нагружения рассматриваются как последовательные ступени нагружения. Таким образом, напряженно-деформированное состояние, полученное для первого случая нагружения, будет исходным для второго  случая, и т.д.
• Напряженно деформированное состояние при нагружении заданной силой показано на рисунке. Здесь Total Translation – полное перемещение, Solid Von Mises Stress – эквивалентное напряжение.  Прогиб рессоры под нагрузкой (перемещение точки приложения нагрузки по оси Y) составляет 280.8 мм. После снятия нагрузки остаточный прогиб составляет 32.6 мм

‍

• Из распределения эквивалентных напряжений мы видим, что почти по всей длине рессоры в верхних и нижних волокнах развиваются напряжения превышающие предел текучести. На первом рисунке приведен график изменения прогиба рессоры по оси Y (T2 Translation), на втором рисунке– график эквивалентных напряжений и пластических деформаций в наиболее нагруженном элементе рессоры по шагам нагрузки и разгрузки рессоры. Точка Set Value=1.0 соответствует действию максимальной нагрузки, точка  Set Value=2.0 соответствует полной разгрузке рессоры. Из первого графика видно, что остаточный прогиб рессоры после снятия нагрузки составляет около 32.5 мм. Из второго графика видно, что после снятия нагрузки в конструкции действуют остаточные деформации, равные пластическим деформациям, и остаточные напряжения. В данном случае ненулевые эквивалентные напряжения в точке Set Value=2.0 вызваны тем, что сжатые волокна рессоры, напряжения в которых во время нагружения превысили предел текучести, после разгрузки растягиваются, и наоборот.