В данной статье мы рассмотрим расширенный нелинейный анализ (SOL 601/701) в программной среде Femap: Advanced Nonlinear Solver на примере тонкостенного цилиндра уделив особое внимание поведению конструкции при потери устойчивости.
Что такое расширенный нелинейный анализ (Advanced Nonlinear Analysis)?
Femap: Advanced Nonlinear Solver представляет собой дополнительный решатель к программному продукту Femap with NX Nastran: Basic.
Данный модуль запускает решатель Adina через NX Nastran. Вы можете найти его в менеджере управления анализом (Analysis Manager), который позволяет быстро и
легко настроить решатель под Ваши задачи.
Femap: Advanced Nonlinear Solver предоставляет дополнительные возможности для нелинейного анализа, которые недоступны в базовом пакете Femap with NX Nastran: Basic.
Модуль расширенного нелинейного анализа поддерживает несколько различных типов решений:
- Неявные статические решения
- Неявные переходные решения
- Явные переходные решения
Возможности нелинейного анализа
Необходимость в использовании Femap: Advanced Nonlinear Solver возникает при появлении геометрической (большие деформации, большие перемещения) и физической (пластичность, ползучесть, вязкоупругость) нелинейностей. Более подробно о разнице между линейной и нелинейной потерей устойчивости мы расскажем в других статьях.
Для анализа физической нелинейности (нелинейные свойства материала) необходимо использовать расширенный нелинейный анализ: например, для анализа модели при переходе из упругой зоны деформаций в пластическую. Вы также можете использовать нелинейный анализ для решения контактных задач (поддерживается контакт типа «поверхность-поверхность»).
В данной статье мы рассмотрим поведение конструкции до и после потери устойчивости при использовании нелинейного анализа Femap: Advanced Nonlinear Solver.
Демонстрация тонкостенного цилиндра
Первая демонстрация представляет собой тонкостенный цилиндр 12,2 м в длину, с основанием 1,83 м и нагрузкой в 861,8 кг.

Как мы увидим ниже, с помощью расширенного нелинейного анализа Femap: Advanced Nonlinear Analysis мы можем определить нагрузку, которая приведет к потере устойчивости. Линейный анализ спрогнозирует потерю устойчивости при нагрузке ~ 3356,6 кг, в то время как расширенный нелинейный анализ поймает нестабильность системы уже при 2177,2 кг.
Функция нагрузки (Load Function)
Сначала рассмотрим задание нагрузки. Как показано ниже, нагрузка в 861,8 кг задается пошагово с помощью временной функции.

Временная функция в данном случае позволит получить процент нагрузки, при котором модель станет нестабильной, т.е. потеряет устойчивость. Как мы видим изменение нагрузки соответствует линейной функции:

Мы используем функцию времени для определения нагрузки на каждом временном промежутке. Нагрузка будет приложена и изменятся в соответствии с временной функцией. Вышеуказанная кривая с каждой секундой изменяет нагрузку на 1%, т.е. 100 секунд - 1х нагрузка (861,8 кг , 100%), 200 секунд - 2х нагрузка (1723,6 кг, 200%), 400 секунд - 4х нагрузка (3447,2 кг, 400%). Настройка данной функции доступна в диалоговом окне Analysis Manager.
Параметры решателя (Analysis Manager, Solver Parameters)

Для выполнения данной задачи мы указываем количество шагов = 400 с приращением на 1 шаг. Таким образом, 1 шаг изменяет 1% нагрузки, 400-й шаг повлечёт за собой изменение нагрузки на 400% (в 4-е раза).

В настройке «Output Every Nth Step» (Вывод каждый n-ый шаг) устанавливаем 2. Таким образом, мы будем получать информацию с результатами через каждый шаг.
Число итераций и сходимость расчета - Iteration and Convergence Parameters (Analysis Manager)
Далее мы рассмотрим число итераций и параметры сходимости расчета. Для установки параметров автоматического пошагового изменения нагрузки нам необходимо включить функцию приращения (по-умолчанию она выключена).

Мы также включаем функцию «Low Speed Dynamic Analysis». Если она у вас включена, убедитесь, что Вам известна масса модели, так как для улучшения сходимости расчета Вам понадобится матрица массы. Масса определяется через плотность.
Результаты линейного анализа потери устойчивости
Сначала мы посмотрим на результаты линейного анализа потери устойчивости. Число 3.9 внизу слева указывает, что коэффициент критической нагрузки равен 3.9 (~ 3356,6 кг), а форма потери устойчивости показана на следующем изображении:

Результаты нелинейного анализа потери устойчивости
При начальном значении в 100% нагрузки (861,8 кг), начинается отклонение и некоторое НДС. Здесь мы видим максимальные перемещения в модели чуть более, чем 78,74 см.

Если бы при линейном анализе, мы увеличили нагрузку в 2-а раза (т.е. 1723,6 кг, шаг 200), мы ожидали бы, что перемещения будут чуть меньше 160 см. Но как мы видим, перемещения увеличиваются больше, чем в 2 раза!

Поэтому мы не можем использовать линейный анализ, т.к. не можем рассчитывать на линейное изменение перемещений относительно изменения нагрузки.
Деформация поперечного сечения
Если внимательно посмотреть на поперечное сечение, то Вы заметите, что оно немного тоньше, чем было изначально.

Это связано с тем, что мы изначально задали идеальную окружность, т.к. размещение плоскости отсечения на поперечном сечении позволяет лучше увидеть его деформацию. Оно потеряло форму окружности и приобрело форму эллипса.
Потеря устойчивости
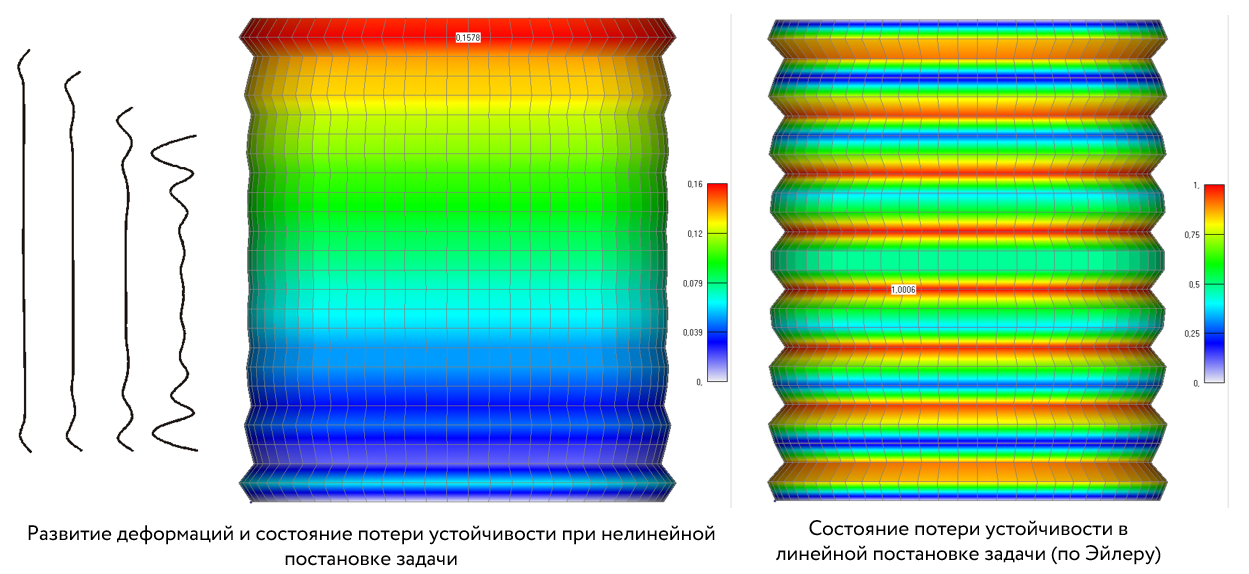
При наращивании нагрузки Вы заметите, что поперечное сечение становится все тоньше и тоньше. А чем тоньше оно становится, тем большее давление оказывается на области, указанные на картинке ниже. С временным шагом 254 (2177,2 кг), вы можете увидеть форму потери устойчивости.

Мы хотели дойти до временного шага 400, но мы уже потеряли сходимость решения на временном шаге 254, это означает, что конструкция не выдержит нагрузки больше, чем 2177,2 кг. Она потеряла устойчивость намного раньше, чем было определено при линейном анализе.
Заключение
Расширенный нелинейный анализ Femap: Advanced Nonlinear Analysis может помочь Вам определить потерю устойчивости вашей модели намного более точно, и даже найти те моменты потери устойчивости, которые не были найдены при классическом линейном анализе.
Во второй части статьи мы проведем анализ потери устойчивости на примере коробчатой рамы конструкции крыла.





.svg)






























.jpg)
.jpg)



