О понимании истинных цветов результатов анализа

Почему вы не всегда получаете то, чего хотите, и как получить то, что вам необходимо

‍

“Всякий раз, когда вы видите эпюру напряжений, просто предположите, что она неверна.” – говорит Марк Шерман (Mark Sherman), глава группы разработки Femap из Siemens PLM Software Solutions. Хотя замечание Шермана и звучит слегка кардинально, это обычная ситуация для сферы численного моделирования, где общепринятым является высказывание “мусор на входе влечет мусор на выходе”. Подобные комментарии ставят вопросы, которые легко сформулировать, но на которые весьма неприятно отвечать даже специалистам.

Каким образом пользователь может быстро проверить достоверность и точность показателей напряжений на конечных элементах модели? Каким образом пользователь сможет ловко доказать посторонним неспециалистам достоверность этих результирующих цветных картинок с высоким разрешением? Истинны ли получаемые данные или нет? Данная статья предоставит вам багаж знаний и средства для защиты результатов ваших расчетов.

Как вычисляются напряжения по МКЭ ?

Давайте посмотрим, что скрывается в концепции КЭ анализа. Как только вы подготовили и запустили расчет вашей КЭ модели, программный решатель вступает в дело. Он берет каждый элемент и расчленяет его на систему уравнений матрицы жесткости. Независимо от того линейные они или нет, эти уравнения комбинируются в матрицу большой размерности, решаются при помощи одного из нескольких численных методов с учетом заданных условий закрепления и нагружения.

При помощи быстрых кликов по пунктам меню и, возможно, после некоторой переориентации модели вы получаете цветную эпюру, которая показывает ... что именно?

Самое время вернуться назад. О чем в большинстве справочных материалов ограничиваются общими словами, так это каким образом решатель формирует уравнения матрицы жесткости от элементов неправильной формы, описываемых в двух или трех измерениях. Это удивительно красивая процедура дискретизации, проходящая в несколько этапов.

Во-первых, каждый элемент разделяется на сектора. Для вычисления примерного объема каждого элемента используется формула взвешивания с применением простых многочленов. Данный этап, известный как интегрирование по Гауссу, является краеугольным камнем всей технологии МКЭ. Без этой процедуры дискретизации не существовал бы МКЭ.

Во-вторых, программа формирует уравнения матрицы жесткости, и решатель накладывает заданные закрепления и нагрузки. Затем решатель вычисляет все перемещения в угловых точках элемента или узлах, что приводит к следующему вопросу: как решатель вычисляет напряжения на некотором удалении от углов элемента?

Ответ на этот вопрос заключается в другом замечательном приеме МКЭ. Теоретиками установлено, что наилучшая зона для определения напряжения в конечном элементе расположена в точках интегрирования Гаусса (центр выделенного сектора). Затем программа из вычисленных перемещений, используя интегрирования Гаусса, определяет сначала деформации, а затем напряжения внутри каждого “Гауссовского объема”. Большинство конечных элементов исследуется с использованием четырех точек интегрирование по Гауссу, и, таким образом, решатель вычисляет напряжения в четырех отдельных точках внутри элемента (см. Рисунок 1).

‍

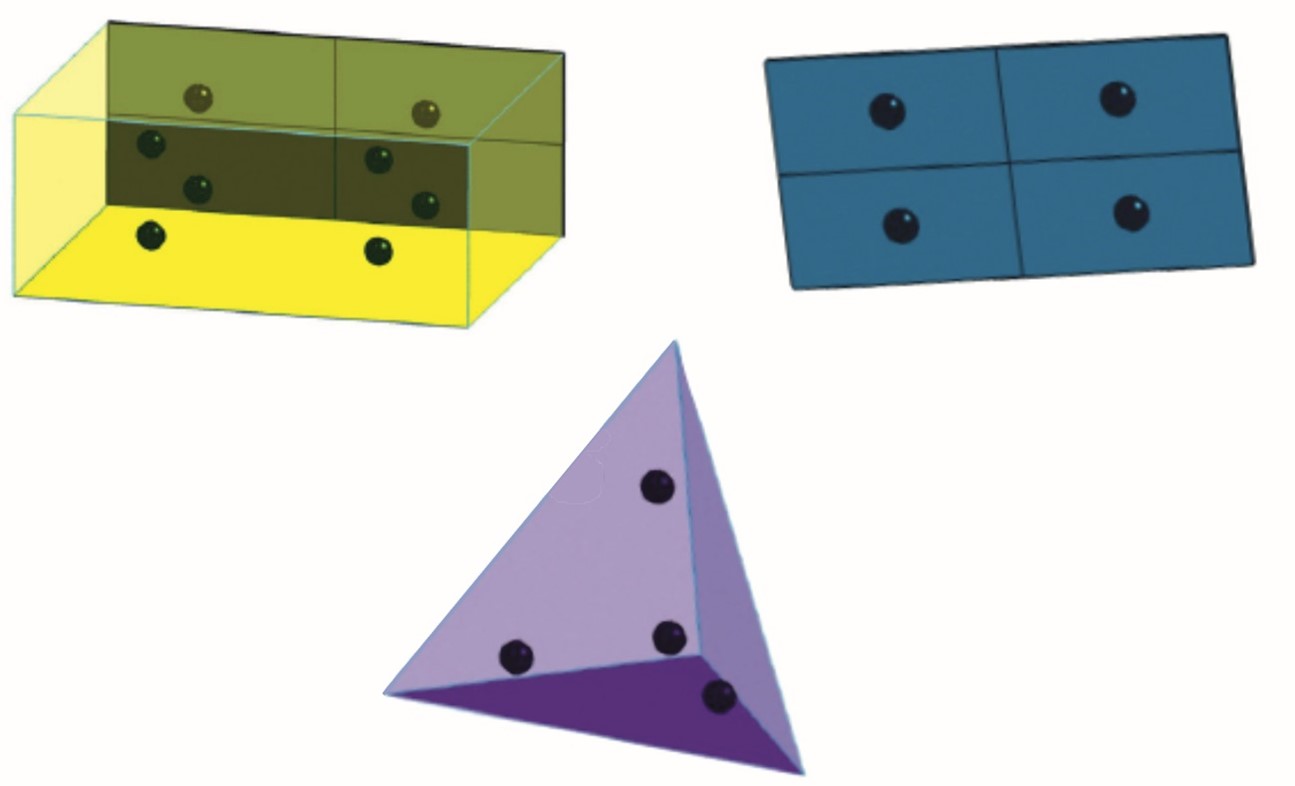
Рисунок 1. Представлены точки интегрирования Гаусса для распространенных форм конечных элементов: пластина, параллелепипед, тетраэдр. Изображения предоставлены Predictive Engineering.

Но каким образом эти точки интегрирования Гаусса соотносятся с тем, что мы видим на реальных эпюрах? Из-за того, что большинство пользователей не хотят иметь дело с необработанными данными от элементов, выполняется еще один финальный этап обработки. Значения напряжений, вычисленные в точках Гаусса, интерполируются в центр элемента, и также экстраполируются из него в угловые точки или узлы. На этой стадии решатель завершает свою работу, и запускается процедура визуализации.

Отладка зубцеобразных эпюр напряжений

Теперь вы более компетентны в том, как вычисляются напряжения, чем большинство специалистов по анализу прочности. Но что именно вы наблюдаете? Эти миллионы экстраполированных точек загружаются в систему графического отображения программы и представляются в виде сияющего и, к тому же, сглаженного цветового спектра. Сглаженный – здесь ключевое слово.

По умолчанию, программные комплексы МКЭ осредняют напряжения в угловых точках каждого элемента и просто представляют осредненные значения пользователю. У этого простого способа сглаживания есть свои преимущества и недостатки. В целом метод хорош, так как он выравнивает значения напряжений для получения гладкой диаграммы. Численно этот процесс делает поправку на нереальные отклонения напряжений, которые образуются из-за незначительных изменений формы элемента.

Так как физические напряжения не являются скачкообразной функцией (стремятся распространяться равномерно), численно осредненные результаты отображают более точное решение. Если это не так, то вы определенно должны забеспокоиться. В этой части и содержится мусор. Должен прозвучать сигнал тревоги, что приводит нас к задаче о совершенствовании ваших способностей в понимании и оценке результатов расчета по МКЭ.

‍

В случае, когда эпюра выглядит зубцеобразной с множеством красных зон (см. Рисунок 2а) или на ней имеются очертания чересчур неправильной формы, для этого наиболее вероятны три причины:

-         неудачно приложены нагрузки и закрепления (вероятно);

-         сложная или некачественная геометрия из CAD-пакетов (неоднозначно); или

-         плохое качество КЭ сетки (см. “Оценка качества формы конечного элемента”).

В связи с тем, что мы используем конечные элементы, чтобы аппроксимировать сплошную среду, иногда бывает лучше всего принять несколько погрешностей, если они могут быть легко объяснены как часть процесса моделирования. Например, можно сослаться на принцип Сен-Венана и сказать, что напряжения и перемещения, возникающие на удалении от точек приложения нагрузки, не зависят от способа приложения этой нагрузки (сосредоточенная или распределенная), так как силы и моменты всегда сохраняются. Другими словами, если исследуемая область находится далеко от зоны приложения нагрузки, то вы можете пренебречь не особо сглаженными напряжениями вблизи точек закрепления.

‍

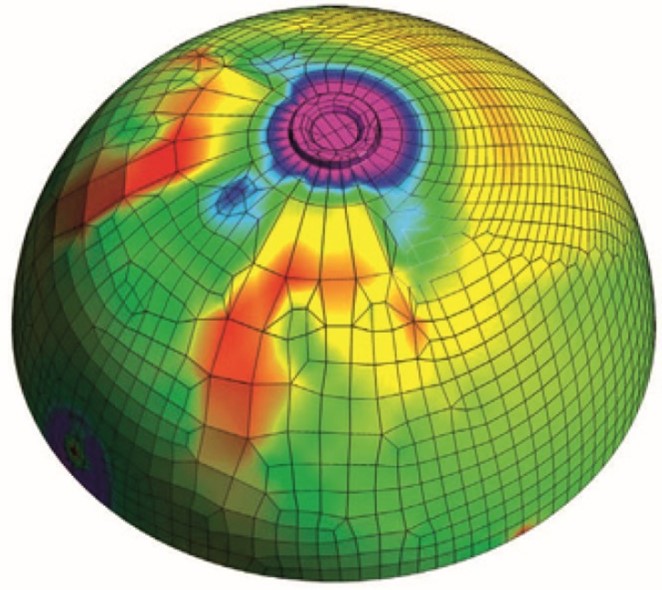
Рисунок 2А – Напряжения никогда не изменяются скачкообразно. Они всегда должны изменяться плавно, поэтому, если ваши напряжения не отображаются должным образом, то, наиболее вероятно, они неверны. В момент, когда вы видите “пятна” высоких напряжений, которые в большом количестве высвечиваются на экране вдоль криволинейной грани данной детали, должна загораться световая сигнализация.

В отношении геометрии конструкторы передают CAD-файлы, которые содержат каждую технологическую деталь вплоть до острых фасок размером

0.005 дюйм или дренажные отверстия малого диаметра для подачи масла. Обычно мы можем (и должны) игнорировать эти малые области, ссылаясь на еще одну полезную закономерность от Жан-Клода Барре де Сен-Венана (см. “Принцип Сен-Венана об ослаблении влияния условий нагружения”, стр. 18). Он установил, что малые конструктивные особенности просто образуют локальные возмущения в поле напряжений. Протяженность этого возмущения составляет не более трехкратного характерного размера малой конструктивной особенности. Например, для отверстий радиусом R этот размер будет 3R. Таким образом, если ваша цель определить общее поле напряжений в конструкции, то локальные отклонения напряжений не будут оказывать влияние на ваш окончательный ответ. Это обстоятельство может быть легко проверено путем проведения двух расчетов одной детали с учетом и без учета нескольких отверстий, а по их окончании подтверждения, что результаты по существу идентичны.

Если же роль малых конструктивных особенностей значительна, и ими нельзя пренебречь, тогда вы должны будете увеличить плотность КЭ сетки таким образом, чтобы результирующее поле напряжений выглядело сглаженным и реалистичным (см. Рисунок 2б). Ваше программное обеспечение сможет без проблем справиться с этой задачей или вы можете обнаружить, что необходимо разделить геометрию на подобъекты, чтобы генератор сетки смог должным образом разобраться с характерными особенностями вашей детали (см. Рисунки 3а и 3б).

‍

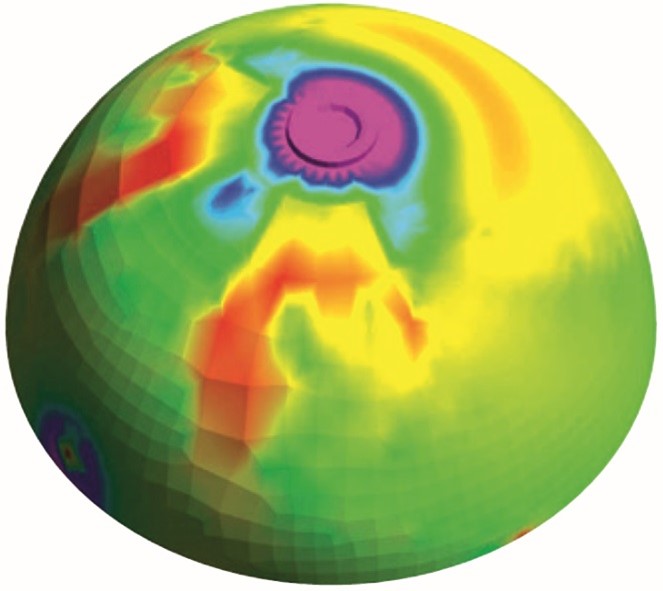
Рисунок 2B – Представленные результирующие напряжения больше на 20%, чем

на Рисунке 2А. Значения характеризуют плавные изменения напряжений на геометрии. При визуальном контроле ясно, что более высокие напряжения отражают результаты, гораздо более близкие к реальности.

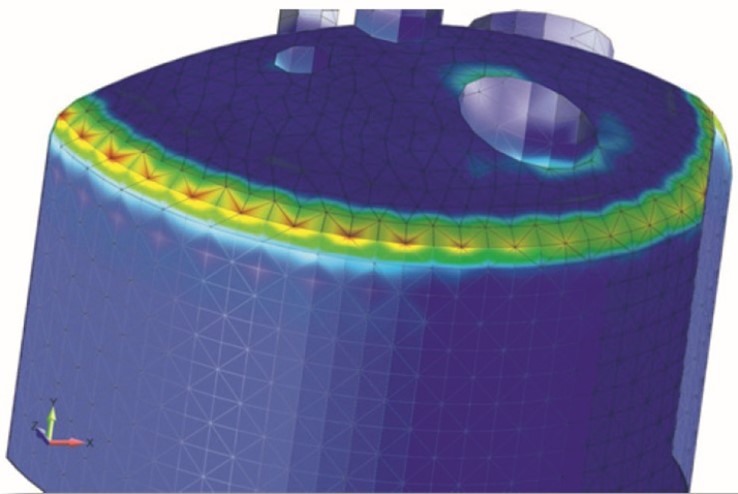
Рисунок 3А (Слева) – Пример плохого построения сетки. Для того, чтобы судить о качестве создаваемых элементов, достаточно просто посмотреть на них. Если области сетки выглядят угловатыми, острыми и нерегулярными, то, наиболее вероятно, получаемые значения напряжений будут неточными. Представленная деталь – это полностью симметричная полусфера (с дополнением в виде малого отверстия внизу слева). Накладываемая сетка в сущности должна быть постоянной на всей детали, но, очевидно, это не так. То же и с напряжениями. Проблема возникает из-за паразитного эффекта алгоритма генерации сетки, и она может быть преодолена путем разделения детали на подобъекты перед операцией наложения сетки.

Рисунок 3B (Справа) – Другой трюк, который поможет вам определить области с некачественной КЭ сеткой, заключается в том, что вам следует выключить отображение границ КЭ сетки, чтобы не знать, где начинаются и заканчиваются элементы. Можно заметить отчетливые колебания уровней напряжений на левой стороне той же полусферической детали несмотря на ее фактическую симметричность.

Интерпретация результатов вычисления напряжений

Сделаем еще одно упоминает об основополагающих принципах. Напряжение равно силе, деленной на площадь. Это главное положение расчета на прочность звучит примитивно, но оно чрезвычайно полезно. Например, если рассмотреть две балки с одинаковым поперечным сечением – одну из алюминия, другую из стали – и нагруженных одинаковой силой, то каждая балка будет испытывать одинаковые напряжения. В докомпьютерную эпоху это обстоятельство было причиной, почему исследователи могли строить из пластмассы масштабные модели сложных конструкций и тем самым получали полезные данные.

Другими словами, если вы прикладываете силу или давление к конструкции, то результирующее напряжение будет зависеть только от геометрического облика этой конструкции и не будет зависеть от материала. В этой связи можно не задумываясь выбрать материал, так как значения наибольших напряжений являются одинаково правильными будь это пластмасса, алюминий или сталь. Единственное, что изменится, – это деформация конструкции, которая меняется совместно с модулем упругости.

При трактовке картины напряжений частым событием является то, что модель выдает очень большие значения напряжений – скажем, 500 МПа, – тогда как пользователь знает, что выбранный для этой конструкции материал (например, низкокачественная сталь) имеет реальный предел текучести 300 МПа.

Как такое происходит? В связи с тем, что КЭ вычисления линейны, решатель не имеет понятия сдеформируется ли материал пластично или разрушится, если превышен предел упругости; он только проводит вычисления на основе геометрического облика и характера нагружения. На этом этапе пользователь должен объяснить получаемый результат. Возможно, что приложенная нагрузка нереально завышена, и в действительности нагрузка должна быть вдвое меньшей. В этом случае ввиду того, что результирующие напряжения линейны, они будут масштабироваться вместе с нагрузкой. По результатам расчета напряжения составят 250 МПа, и конструкция не разрушится (см. Рисунок 4).

‍

Рисунок 4 – Иногда кажется, что полученные результаты не имеют смысла, но они достаточно правдоподобны при их корректной интерпретации. Представленный хирургический упор имеет предел текучести около 100,000 фунт/дюйм2. При вычисленных напряжениях более 200,000 фунт/дюйм2 деталь уже разрушится. Это обстоятельство демонстрирует достоинство знаний о визуализации – вы знаете, что “неплохо – это довольно-таки хорошо”, и переразбиение сетки будет только пустой тратой времени.

Визуализация за пределами концепции МКЭ

Множество других методов анализа (например, численная механика жидкости и газа) также используют КЭ сетку, чтобы покрыть области пространства. Во всех случаях численный решатель пытается зафиксировать плавно изменяющееся поле будь то течение жидкости или электромагнитное явление. И если накладываемая сетка выстроена гладко, тогда естественным путем будет получаться качественное решение. Человеческий глаз является мощным инструментом для распознавания регулярности сетки, так как нерегулярность часто свидетельствует об опасности или скрытых ошибках. Одним словом, держите вашу сетку гладкой и регулярной, позвольте вашим глазам осуществлять критичную оценку, и в дальнейшем вы будете чувствовать себя увереннее при проведении численных расчетов.

Оценка качества формы конечных элементов

Интегрирование по Гауссу является точным методом только для элементов, форма которых близка к идеальной – соотношение сторон 1x1 для пластин или 1x1x1 для твердотельных элементов (например, параллелепипеды и тетраэдры). Как только форма элемента начинает ухудшаться, то же начинает происходить и с добротностью ваших результатов.

Проверенным способом контроля является обстоятельство, когда форма элемента будет “радовать глаз” и сохранять это единообразие по всей модели. Хотя это и субъективный подход, если сетка оказывается близкой к пропорциям 1x1x1, то вы на правильном пути.

Принцип Сен-Венана об уменьшении влияния способа нагружения

В 1855 году французский теоретик в области упругого деформирования

Жан-Клод Барре де Сен-Венан сделал заключение, что эффекты от механического нагружения тела быстро убывают по мере удаления от точки приложения нагрузки – на расстояниях, сопоставимых с размерами детали. В 1945 году Рихард Эдлен фон Мизез вывел математическое описание этого эффекта при помощи дифференциальных уравнений в частных производных.

Данный принцип позволяет КЭ алгоритмам заменять сложные распределения напряжений простыми до тех пор, пока границы малы. Вы можете сравнить это положение с эффектами электростатического поля, когда поле угасает на расстояниях , где i соответствует числу полюсов.