Моделирование многослойного КМ в FEMAP

В этом разделе мы подробно расскажем о моделировании многослойных композиционных материалов(КМ) в Siemens Femap. Существует 4 основных отличия от моделирования металлических деталей. Необходимо знать следующее:

• Свойства материала (ортотропный или анизотропный и т.п.)
• Количество слоев, их толщину и углы укладки материала по отношению к оси элемента(reference axis)
• Тип элемента (Laminate) и свойства материала (2D или 3D – Orthotropic)
• Направление, относительно которого будем откладывать углы укладки слоев.

Каждый из указанных выше пунктов рассмотрим в Femap далее. Есть два способа, которые можно использовать для моделирования многослойных композитов в Siemens Femap. Зависит от того, является ли модель двумерной или трехмерной. Определение материала, конфигурации слоев (Layup) и свойств (Property) является общим для двумерных и трехмерных моделей. Однако, углы укладки слоев могут быть заданы с использованием двух методов для 2D-модели, в то время как для 3D-модели используется лишь один метод. В двумерной модели углы укладки можно задавать направлением элементов или непосредственно в свойствах. Определение углов укладки материала на элементах - удобный подход, особенно при сложной геометрии. Можно выбрать несколько элементов и задать углы укладки материала вместо назначения определенного угла материала всем элементам в свойствах. Для 3D-моделей мы должны задавать углы укладки слоев в свойствах, поэтому для моделей со сложной геометрией нужно создавать несколько свойств. В следующих подразделах приведен обзор функций Siemens Femap для моделирования многослойного композита с примерами.

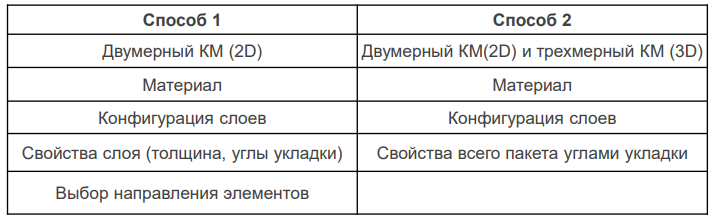
Существенные параметры

Моделирование может быть простым, если грамотно задать параметры композиционного материала.

Важно выбрать (или создать) систему координат, которая подходит для вашей модели. В большинстве случаев подойдет базовая прямоугольная система координат. Тем не менее, нужно быть осторожным при работе с композиционными материалами (КМ) на криволинейных поверхностях. Углы укладки отдельных слоев, назначенные в редакторе конфигурации пакета(layups), будут откладываться от начальной системы координат.

Следует назначить тип материала (Materials) для многослойного КМ. Есть двумерные или трёхмерные ортотропные материалы.

Должны быть указаны свойства КМ (Properties). Для двумерных элементов используют свойство «Laminate». Аналогично, для 3D-элементов используют «Solid Laminate». Также в свойствах можно указать подходящий критерий разрушения (Failure Criterion).

Углы укладки, толщины, количество слоев и их направление задают в редакторе конфигурации слоев (Layups).

Всегда проверяйте свои единицы измерения

Определение ортотропного материала

• Обратите внимание, что свойства материала в продольном и поперечном направлениях разные.Продольное направление определяется углом укладки.
• В зависимости от типа анализа требуются различные свойства материала.

Выберите подходящий тип материала (например, Ortotropic 2D):

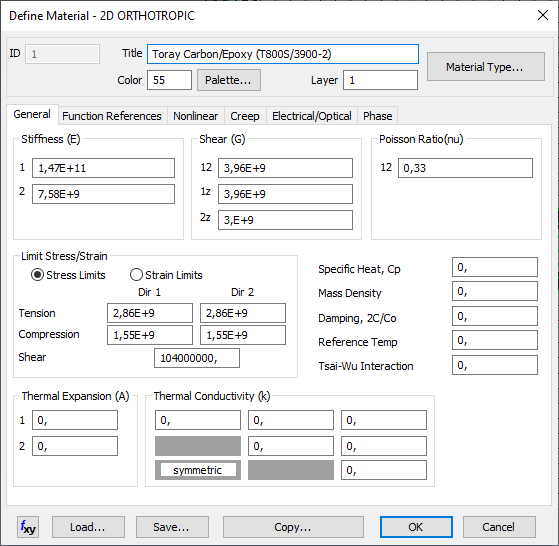
Опция Tsai-Wu Interaction требуется, если используется критерий разрушения Цая-Ву (Tsai-Wu). Это значение должно быть определено экспериментально. Если у вас есть свойства волокна и матрицы, можно оценить свойства композита, используя правила смесей или другие методы.

Общие сведения о редакторе конфигурации слоев (Layup)

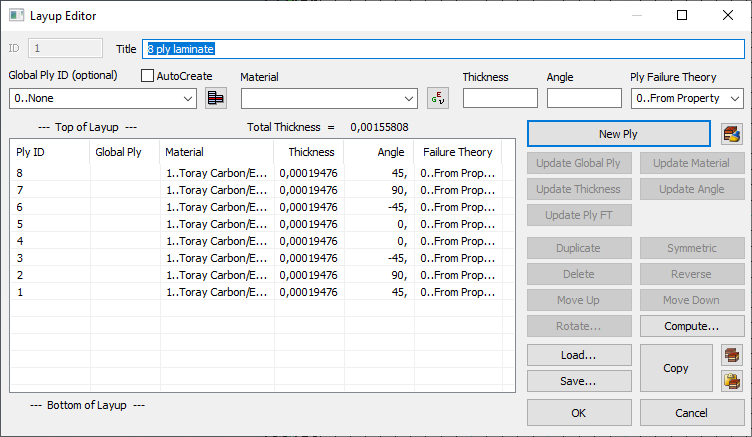
• Обратите внимание на нумерацию слоев пакета укладки; Она начинается с нижнего слоя.
• Материал, назначенный для каждого слоя. Можно также назначить несколько материалов(например, материал сотового заполнителя).
• Углы укладки задаются относительно оси ориентации материала.
• Кнопка Compute вычисляет эквивалентные свойства пакета (мембранные свойства, изгибные свойства, ABD матрицу – матрицу жесткости)
• В поле Thickness задается толщина элементарного слоя

Средство просмотра структуры пакета - это полезный инструмент для визуализации структуры слоёв:

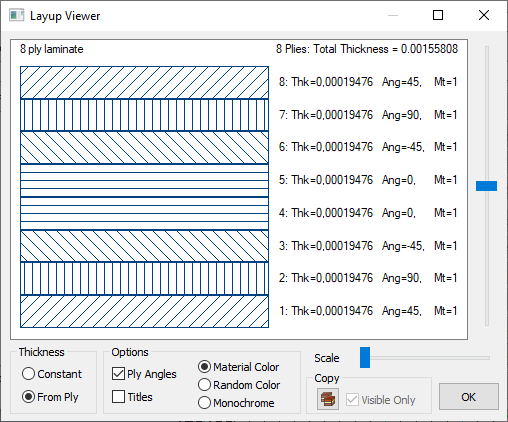
Важно отметить, что отображаются углы ориентации слоев относительно оси ориентации материала (указанного в свойстве или для элемента). Чтобы избежать путаницы, можно отобразить ориентацию вдоль элемента с заданным углом и убедиться, что углы соответствуют фактической ориентации пакете.

Свойства (Property): Моделирование двумерного композиционного материала

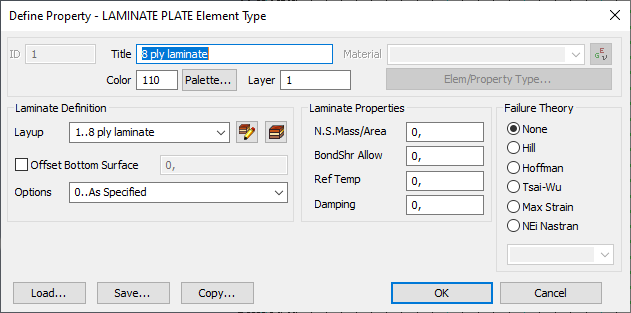
• По умолчанию толщина откладывается от срединной поверхности
• Если все слои в композите описаны в редакторе слоев, вы можете оставить все по умолчанию. Если описана только половина слоев, Вы можете использовать опцию симметрии для создания симметричной структуры КМ
• Параметр bondShr Allow требуется, если выбран критерий разрушения. Это допускаемое напряжение межслоевого сдвига
• Используйте определенную теорию разрушения материала, если хотите вычислить критерий разрушения для отдельных слоев
• Назначьте соответствующий угол оси материала. Углы волокон слоев будут ориентированы относительно этой оси

Углы укладки материала и главное направление

Если углы укладки определены в редакторе слоев, то Femap не будет знать, с какого направления отсчитывать эти углы. Поэтому нужно задать главное направление ориентации материала. Это будет базовый вектор, указывающий продольное направление материала. Например, если выбран базовый вектор по оси X, тогда при ориентации всех слоев будет происходить по направлению оси X (это будет продольное направление, соответствующее углу 0 градусов). Не следует путать термины «угол укладки материала» и «направление ориентации» в редакторе слоев. Угол укладки материала - это угол, между заданным базовый направлением и направлением укладки волокон материала. Главное направление - это ось, от которой откладывается угол укладки. По умолчанию Femap не назначает никакого угла материала. Для задания угла материала используйте любой из следующих способов.

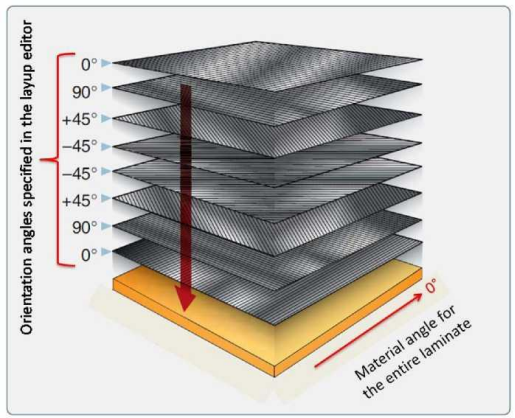
Задание базового направления, ориентации элементов

Можно определить или изменить направление элементов, используя команду Modify, Update Elements, Material Orientation:

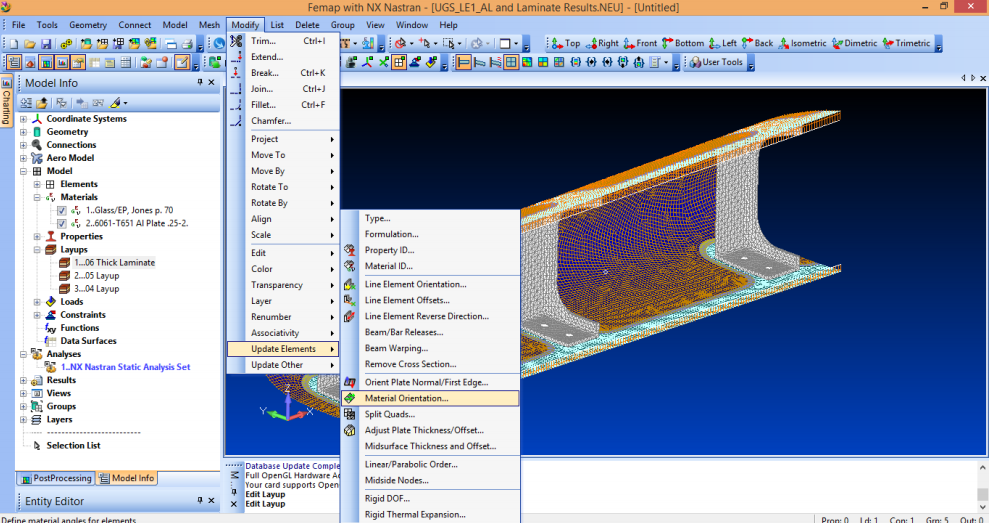
Этот метод позволяет задать базовое направление для выбранного набора элементов или всех элементов за один раз. Важно отметить, что это направление не зависит от системы координат элемента и формы элемента. Например, на рисунке ниже показаны элементы, форма которых искажена. Однако все углы материала выравниваются по направлению глобальной оси X. Если угол материала не определен, Femap при выполнении трансляции во входной файл Nastran выведет сообщение об ошибке. Если вы не определите направление для нескольких элементов в модели, может быть довольно сложно отследить элементы с пропущенными определениями направлений. Углы материала в элементах Laminate можно проверить, выбрав следующие параметры, используя F6 или команду View Options.

Далее мы покажем, как отобразить базовое направление. Можно также проверить заданные направление и обновить его, если изменяли, используя процедуру, описанную ранее. В случае сложной геометрии с криволинейными поверхностями, базовое направление материала может быть эффективно определены с помощью цилиндрической системы координат, если базовый вектора должен следовать по касательной к поверхности.

Пример определения направления материала для модели со сложной геометрией

На следующей картинке показан носок композитного крыла. Направление материала вдоль оси должно соответствовать кривизне на передней кромке. Однако из рисунка видно, что векторы, представляющие вектор направления материала, не следуют за кривизной.

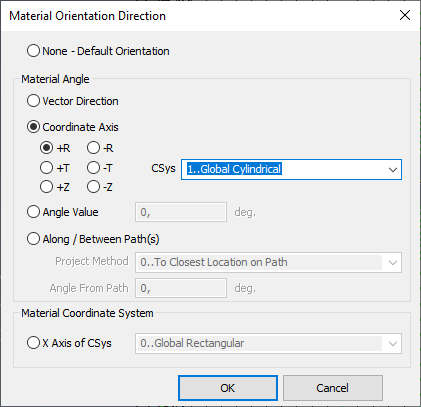
Чтобы точно учесть угол материала, мы можем использовать цилиндрическую систему координат (R, T, Z) вместо прямоугольной системы координат (X, Y, Z). Мы хотим создать новую цилиндрическую систему координат вместо существующей цилиндрической системы координат, которая будет корректно выдерживать направление материала. Для создания новой цилиндрической системы координат выполните следующие шаги:

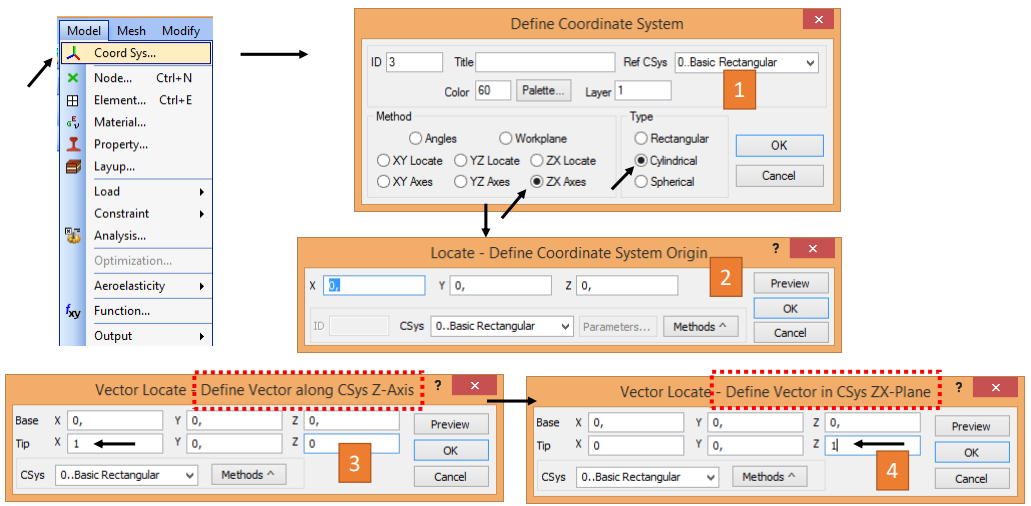
Мы будем использовать процедуру, описанную ранее в разделе "Задание базового направления, ориентации элементов", чтобы обновить направление материала. Выполните команду Modify, UpdateElements, Material Orientation. Вам будет предложено выбрать элементы, для которых должен быть определен/обновлен угол материала. В этом примере мы выберем все криволинейные элементы. Затем Вам будет предложено выбрать направление ориентации материала, как показано ниже.

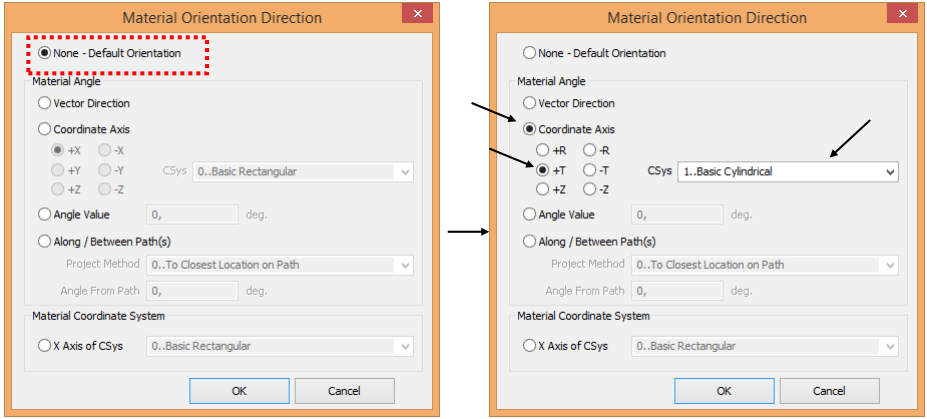
Описанная выше процедура будет ориентировать все углы материала вдоль кривизны передней кромки.

Создание свойств трехмерного композиционного материала

Обратите внимание, что выбор теории разрушения недоступен в окне свойств. Для 3D композитов критерий разрушения указывается при выборе материала:

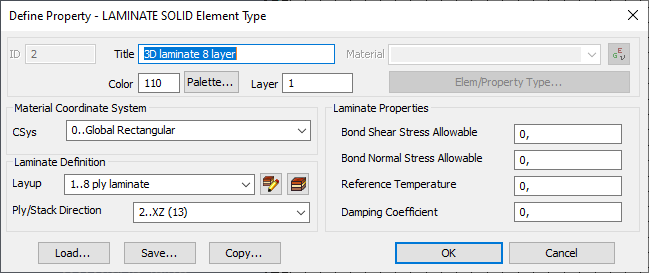
При моделировании 3D композитов указываются как сдвиговые (Shear), так и нормальные (Normal) допускаемые напряжения в связующем материале.

При моделировании трехмерного КМ определяется направление пакета (ply/stack) вместо направления материала. Например, если направление материала задано осью Х глобальной системы и пакет укладки ориентирован в направлении Z, то мы указываем направление пакета как XZ (13). В отличие от 2D, мы не можем использовать подход 1 (Modify, Update Elements, Material Orientation) для 3D laminate элементов. Мы можем создать несколько свойств (если необходимо) с разными направлениями пакетов для различных секций геометрии. Попробуйте исследовать другие системы координат для задания направления пакета.

Пример определения направления пакета в трехмерной композиционной конструкции

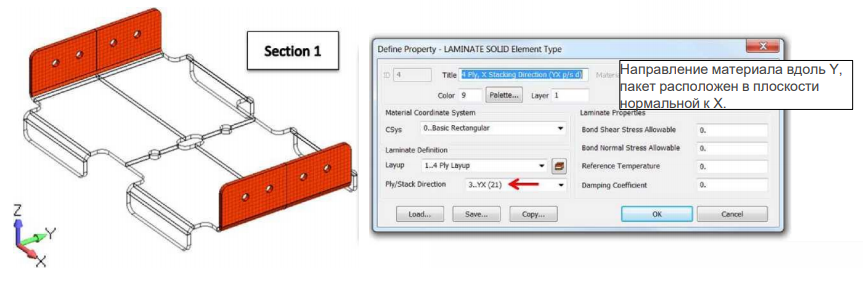
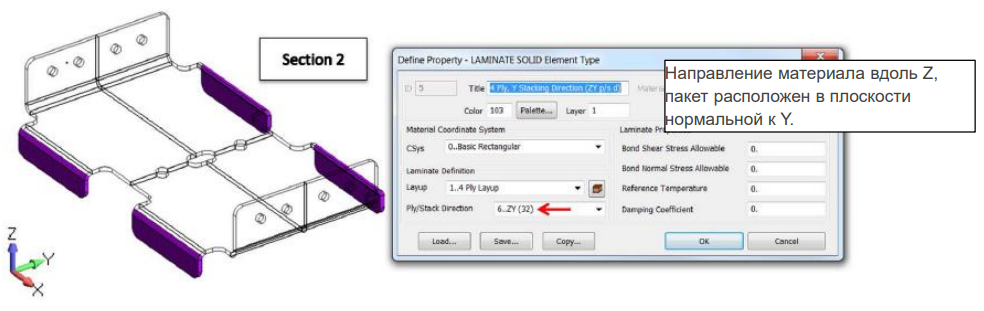
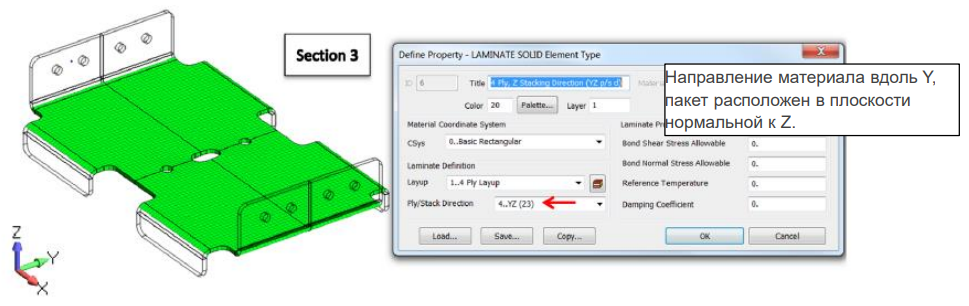
В этом примере показана композитная деталь с секциями, ориентированными в разных направлениях. Деталь моделируется с использованием 3D элементов. Здесь мы не можем использовать одно направление пакета для всех секций детали.

В этом примере мы создадим три различных свойства, обозначенных различными цветами, как показано выше,чтобы определить направление пакетов отдельно для каждой из трех секций композитной детали. Следующие изображения покажут, как были определены направления пакетов для этих секций:

ПРИМЕР №1. СОЗДАНИЕ ДВУМЕРНОЙ МОДЕЛИ ИЗ КМ В FEMAP

Введение

В этом примере мы выполним анализ простого двумерного композита с отверстием под действием одноосного растяжения. Подобные композитные конструкции с отверстиями часто применяются в аэрокосмической промышленности. Материал, укладка слоев и их толщина, используемые в этом примере, не абстрактная, а реально используемая в отраслях промышленности. Рассмотрим два пакета с одинаковым количеством слоев и одинаковой ориентацией, но уложенных по-разному. Проанализируем различия в результатах, просто изменив порядок укладки. Работая с примером, изучим уникальное поведение композитов.

Создание свойств материала

Свойства материала, используемые для композита, соответствуют пластинке из однонаправленного углеродного волокна, пропитанной эпоксидной смолой. Соответственно, для этой задачи тип материал должен быть «2D Orthotropic». Свойства материала приведены в следующей таблице:

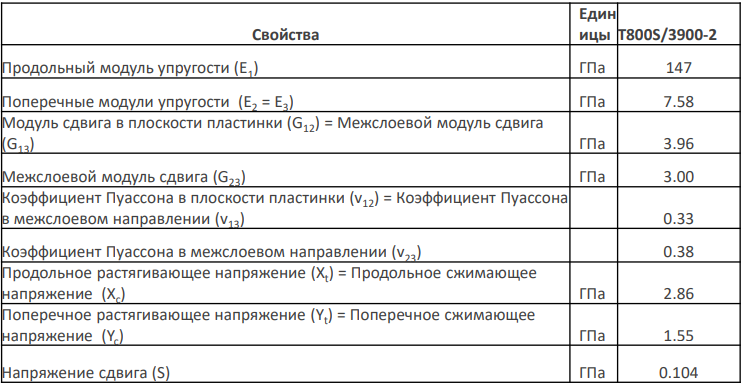
Поскольку в этой задаче модель композита двумерная, свойствами материала в направлении 3 можно пренебречь.

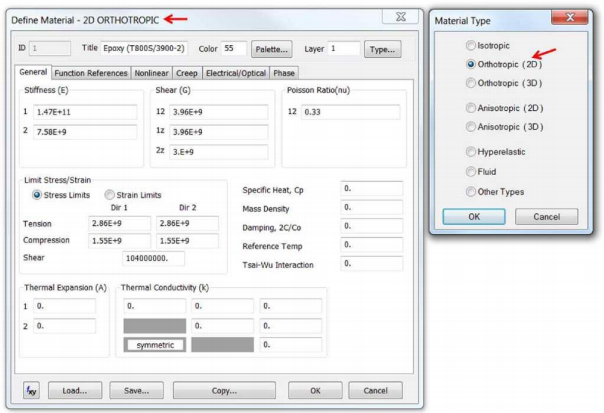
Задание пакета укладки

В этой модели мы проанализируем два вида пакета с разной укладкой слоев. Идея состоит в том, чтобы исследовать, как укладка слоев может повлиять на результаты анализа, даже если композит имеет одинаковое количество слоев, слои имеют одинаковые углы ориентации, но сложены в другой последовательности.

Пакет укладки 1: [45°/90°/45°/0°]s каждый слой толщиной 0.195 мм. Нижний индекс 's' в определении укладки указывает на то, что пакет является симметричным ламинатом. Это означает, что конфигурация пакета следующая: [45°/90°/-45°/0°/0°/-45°/90°/45°].

Пакет укладки 2: [45°/90°/-45°/0°/45°/90°/-45°/0°]. Пакет 2 имеет 8 слоев так же как пакет 1, за исключением того, что конфигурация пакета больше не симметрична относительно срединной плоскости ламината. Редактор пакета с определением Пакета 1 показан ниже. Пакет 2 можно определить аналогичным образом, изменив углы ориентации:

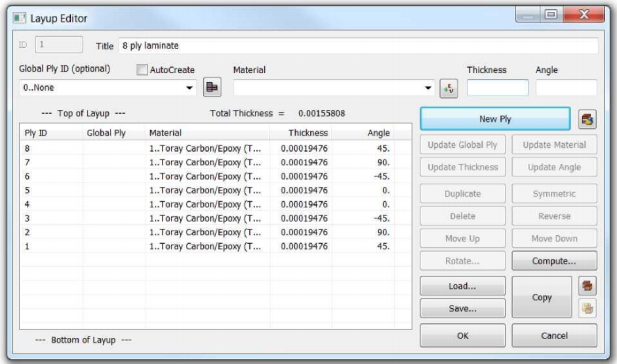
Определение свойства композита (PCOMP)

За свойства 2D композитов в Nastran отвечает функция PCOMP. Подробная информация о функция PCOMP доступна в руководстве пользователя Nastran (Nastran User Guide). Модель двумерного композита основана на классической теории композитов. Выберите тип «Laminate» по кнопке Element/Property Type. По умолчанию Femap назначает тип элемента «Plate» для 2D-моделей. Пакет (Layup), определенный на предыдущем шаге, можно назначить при задании свойства композита. Поскольку мы определили все 8 слоев в пакете укладки, в окне Свойств (Property) в списке Options оставлено по умолчанию "0. As Specified". В качестве альтернативы, мы можем определить только 4 слоя в пакете и использовать опцию "1. Simmetric". Однако этот параметр следует использовать с осторожностью, поскольку его нельзя использовать для несимметричного композита.

Задание направления материала

Для этой задачи мы будем использовать направление по глобальной оси X в качестве базового направления материала. Мы можем использовать одну из процедур, которые были описаны ранее.

Параметры анализа и пост-процесса

Для этой модели сила 10 кН приложена к узлам на одном конце, а узлы на другом конце закреплены, как показано ниже. Чтобы имитировать поведение нагрузки в эксперименте, нагрузка 10 кН прикладывается к независимому узлу Rigid-элемента и этот узел связан с узлами на правом конце панели (см. ниже). Когда нагрузка прикладывается к независимому узлу, его перемещение преобразуется в соответствующие перемещения зависимых узлов.

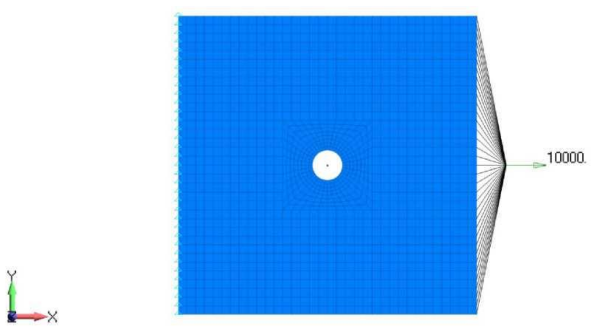
Модель готова для анализа и для нее получено линейное статическое решение. Анализ модели выполнен для двух пакетов укладки и мы проанализируем напряжения, наблюдаемые в обоих этих случаях.

НАСТРОЙКА ДИСПЕТЧЕРА АНАЛИЗА (ANALYSIS SET MANAGER) ДЛЯ КОМПОЗИТОВ

• Параметр SRCOMPS управляет вычислением и выводом коэффициентов прочности слоев. Если флаг включен, для элементов композита выводятся коэффициенты прочности слоев, если задан критерий разрушения.
• Параметр NOFISR управляет вычислением и выводом индексов разрушения и коэффициентов прочности слоев. Если флаг включен, индексы разрушения и коэффициенты прочности слоев не выводятся в файл f06.

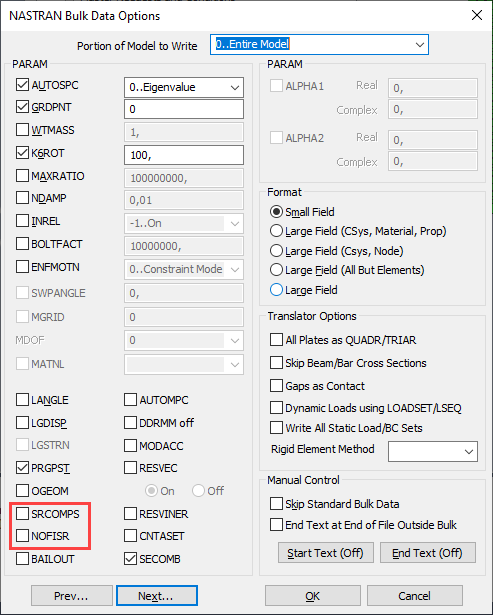
Обработка и вывод результатов

Вначале проанализировали модель с симметричной укладкой слоев ([45°/90°/45°/0°/0°/45°/90°/45°]). Общие перемещения этой модели показаны ниже. Деформации симметричны относительно оси X. При приложении одноосной растягивающей нагрузки деформации панели лежат в плоскости, как и ожидалось. Не наблюдается никаких деформаций из плоскости пластины. Затем была проанализирована модель с несимметричной укладкой слоев ([45°/90°/-45°/0°/45°/90°/-45°/0°]). Из линий уровней (показанных ниже) можно заметить, что деформации не симметричны относительно оси X. Кроме того, теперь мы можем видеть, что несимметричный слоистый материал привел к деформациям из плоскости пластины, хотя нагрузка была одноосной.

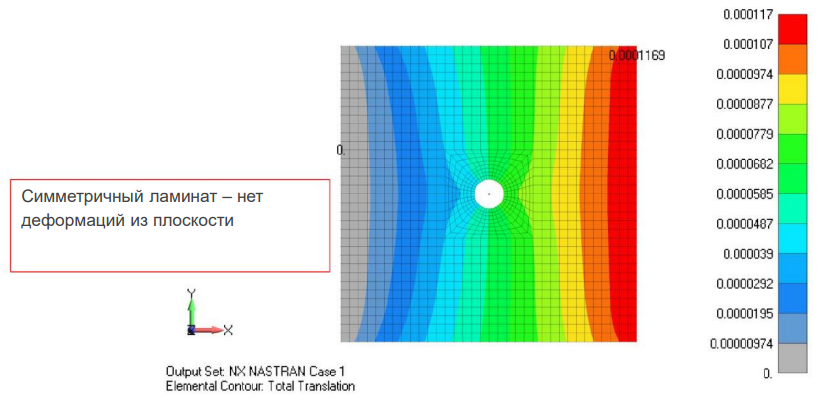
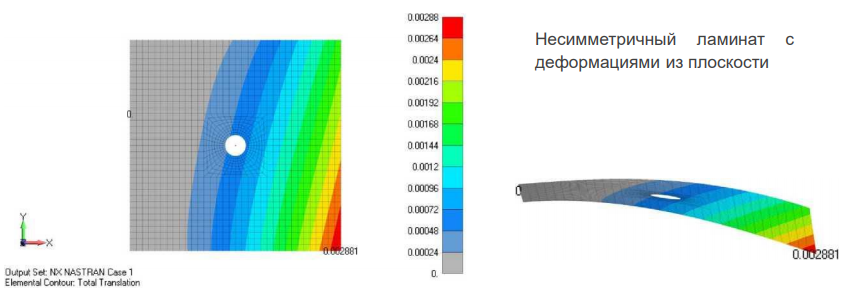
Такое поведение присуще только композитным панелям армированным волокном, и часто не исследуется из-за проблем с их проектированием. Несимметричная укладка может привести к деформации ламината уже во время производственного процесса, при отверждении ламината при высоких температурах.

Таким образом, довольно сложно спроектировать несимметричный ламинат, соответствующий конкретному нагружению. Один из практических примеров использования несимметричного ламината - это композитные крылья обратной стреловидности самолетов Х-29 и Су-47.

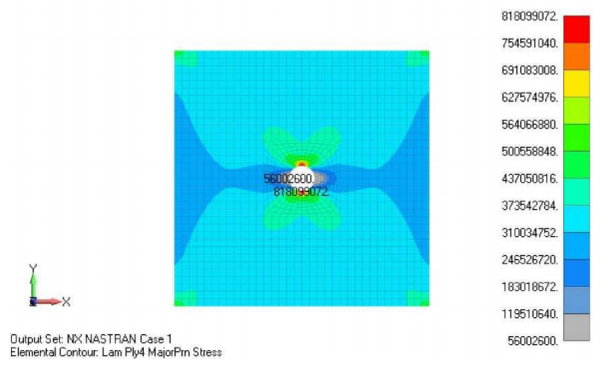
Линии уровней напряжений, показанные выше, соответствуют наибольшему главному напряжению (Major Principal Stress) в слое 4 (слой 0°). Аналогичным образом мы можем построить распределение напряжений в других слоях. В Femapимеется множество векторов вывода, и иногда бывает сложно найти тот же вектор вывода для другого слоя. В Siemens Femap есть несколько специальных инструментов, которые можно эффективно применять для панелей из КМ. Например, мы можем использовать инструмент «Laminate Prev Ply» для построения Major Principal Stress для слоя 3, при условии, что у нас есть отображение Major Principal Stress для слоя 4, не прилагая усилий для нахождения выходного вектора среди большого набора результатов. Это будет особенно полезно, если у вас есть большое количество слоев в ламинате. Ниже перечислены некоторые из инструментов, предназначенных для ламинатов. Доступ к этим инструментам осуществляется из меню Custom Tools, PostProcessing.

ПРИМЕР №2. СОЗДАНИЕ ТРЕХМЕРНОЙ МОДЕЛИ ИЗ КМ В FEMAP

Введение

В этом примере мы разработаем трехмерную модель для анализа простого композитной панели с отверстием, подвергнутого одноосному растяжению. Это дополнение к первому примеру для 3D композитной модели. Цель состоит в том, чтобы сравнить обе модели. Материал, укладка, толщина и подход, используемые в этом примере, такие же, как в примере 1. Основное различие между 3D моделью и 2D моделью заключается в том, что в первой модели, в отличие от второй, вычисляются и учитываются поперечные напряжения. Модели из 3D-ламината будут полезны, если вы моделируете композитную конструкцию со «открытыми» кромками, такими как отверстия, в которых могут иметь значение поперечные и сдвиговые напряжения.

СОЗДАНИЕ СВОЙСТВ МАТЕРИАЛА

Определение свойств материала трехмерной модели аналогично двумерной модели, за исключением того, что тип материала теперь 3D-ортотропный (3D Orthotropic). Соответственно, должны быть заданы свойства в трех направлениях. Все необходимые свойства определены в таблице 1.Задание слоев укладки. Задание конфигурации укладки аналогично двумерному. Однако свойство материала (трехмерное ортотропное), созданное на предыдущем шаге, должно использоваться вместо двумерных ортотропных свойств, как в примере 1.

Задание свойства ламината (PCOMPS)

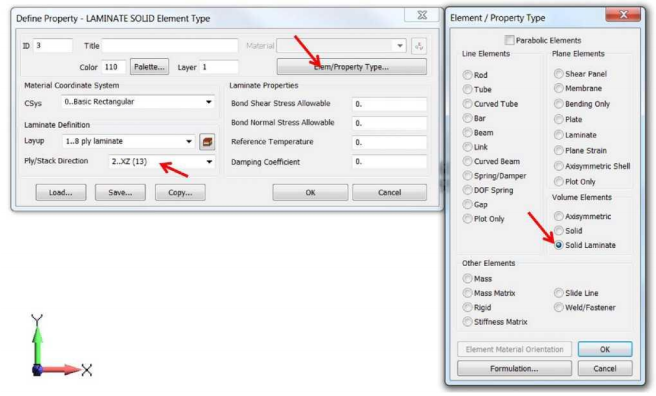
За свойства трехмерных композитов в Nastran отвечает функция PCOMPS. Подробная информация о ней доступна в Руководстве пользователя Nastran (Nastran User Guide). Выберите в окне задания свойств по кнопке Element/Property Type «Solid Laminate». По умолчанию Femap назначает тип элемента Solid для 3D моделей. Задание укладки слоев, выполненное на предыдущем шаге, можно назначить в окне задания свойств. Интерфейс окна задания свойств 3D-композита немного отличается от 2D. Здесь должно быть назначено направление пакета «Ply / Stack Direction». Например, для трехмерной модели направление Ply /Stack (Слой/Пакет) задается как «XZ (13)». Здесь «X» соответствует направлению материала (как определено в 2D-случае), а ось «Z» - это нормаль к направлению укладки. В отличие от двумерных ламинатов, трехмерный композит не основан на классической теории ламинатов.

Определение углов материала

Единственное различие между заданием углов материала для 2D-случая и трехмерного случая состоит в том, что для 3D-модели требуется указать направление «Ply / Stack». Общая концепция остается той же.

Обработка и отображение результатов

На изображении ниже показана сетка конечных элементов трехмерной модели композита. В этом примере задан только один объемный (Solid) элемент по толщине пластины. Толщина элемента соответствует общей толщине пакета 1,56 мм.

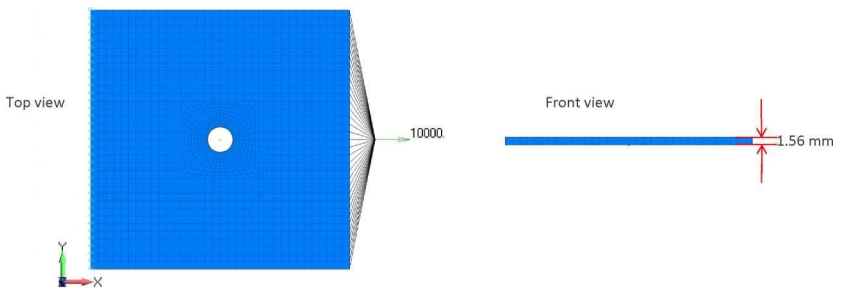
Анализируется модель с симметричной конфигурацией пакета укладки. Полученные перемещения и напряжения показаны ниже. Результаты по перемещениям очень похожи на двумерный случай.

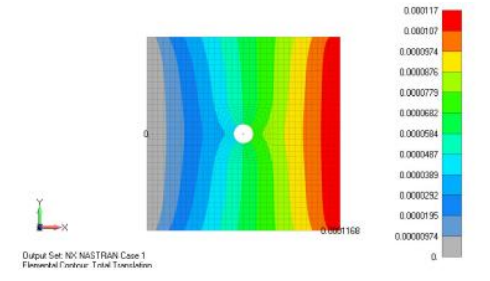
Ниже показано распределение максимальных главных напряжений в слое 4 (слой 0°):

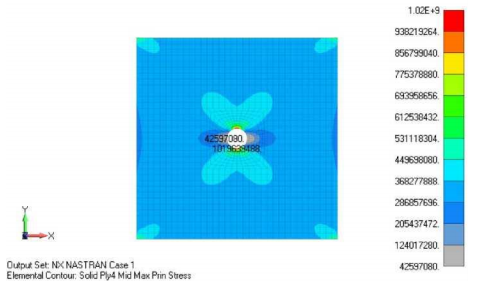
ПРИМЕР №3. МОДЕЛИРОВАНИЕ СЭНДВИЧ КОМПОЗИТА (ТРЕХСЛОЙКИ)

Введение

В этом примере анализируется трехмерная композитная трехслойная модель нагруженная равномерным давлением. Сэндвич-композиты имеют центральный слой (Core) - заполнитель, например, сотовый, из пенопласта и т.п., расположенный между двумя несущими панелями (Facesheet). Как правило, несущие панели несут большую часть нагрузки в плоскости композита и воспринимают изгибные нагрузки, в то время как заполнитель воспринимает сдвиг. Сэндвич-композит можно легко смоделировать, используя двумерные укладки слоев композита, определив заполнитель как один из слоев в редакторе пакета укладки, как показано в конце этого примера. Эта процедура проста, однако межслоевые сдвиговые напряжения, действующие между слоев,становятся важными в сэндвич-композитах, а двумерные модели композита, основанные на классической теории композитов, не учитывают напряжения в плоскости.

Создание свойств материала

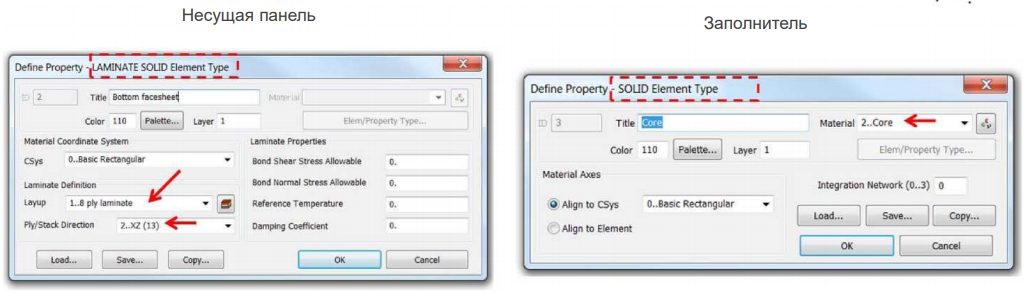
Создаем два материала для несущих панелей и для заполнителя. Композитные несущие панели моделируются трехмерным ортотропным материалом, его свойства показаны в таблице 1 (Пример 1). Заполнитель моделируется изотропным материалом с E = 4 ГПа и v = 0,25 [3].

Определение укладки пакета

Укладка пакета для несущих панелей такая же, как во втором примере. Однако следует отметить, что у насесть две несущих панели, поэтому мы должны создать два свойства трехмерного (Solid) ламината, одно для верхней панели и одно для нижней. Если две укладки пакета не создаются отдельно для каждой несущей панели, мы увидим в наборе результатов выходные векторы, соответствующие только 8 слоям укладки. Если создаются два пакета укладки, мы можем видеть выходные векторы для 16 слоев, 8 для нижней панели и 8 для верхней.

Определение свойств модели

Должны быть созданы три свойства: два свойства для несущих панелей и одно свойство для заполнителя. Каждое свойство должна быть назначено для соответствующей несущей панели. Назначение направление пакета для трехмерной модели композита аналогично предыдущему примеру.

Отображение результатов

Края сэндвич-панели были закреплены по всем направлениям, и к верхней поверхности было приложено давление 1 МПа:

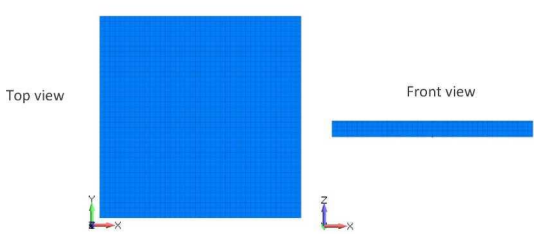
Контурные лини перемещения после приложения давления показаны ниже:

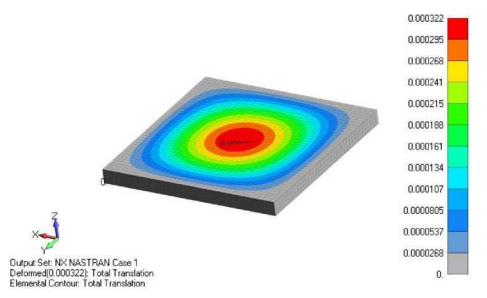
Распределение межслоевых сдвиговых напряжений в заполнителе показано ниже. Можно скрыть элементы несущей панели при построении распределения напряжений сдвига в заполнителе:

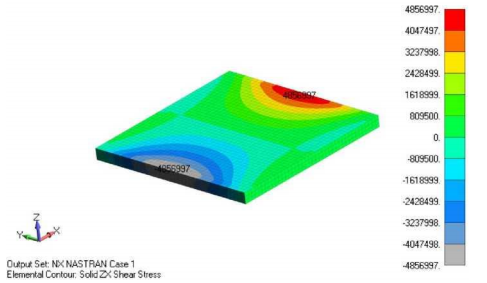
Граница между заполнителем и несущими панелями является одним из критических участков с точки зрения расслоения сэндвич-композитов. Межслоевые сдвиговые напряжения выше на краях, и эти участки являются потенциальными для инициирования расслоения. Можно сравнить межслоевые сдвиговые напряжения с допускаемым сдвигом материала, связующего заполнитель с несущими панелями и проанализировать возможное расслоение.

Другие методы моделирования сэндвич-композита

В этом примере мы создали 3D-модель сэндвич-композита, в которой несущие панели (Facesheets) и заполнитель (Core) моделируются твердыми телами. Другими методами, с помощью которых можно решить эту задачу, являются:

1. Двумерное моделирование сэндвич-композитов , в котором и несущие поверхности и заполнитель являются двумерными, и могут быть заданы в одном пакете укладки. Это удобный подход, однако, как обсуждалось ранее,двумерные многослойные модели основаны на классической теории композитов и не учитывают напряжения вне плоскости композита . Для оценки межслоевых напряжений используют другие методы.
2. Смешивание двумерной модели композита и трехмерного заполнителя. В этом методе несущие панели могут быть смоделированы двумерными элементами «Laminate» , а заполнитель может быть смоделирован как твердое тело. Нужно быть осторожным при задании панелей в этой конфигурации. Обе несущие панели должны быть расположены со смещением равным половине толщины композитной панели от трехмерного заполнителя.

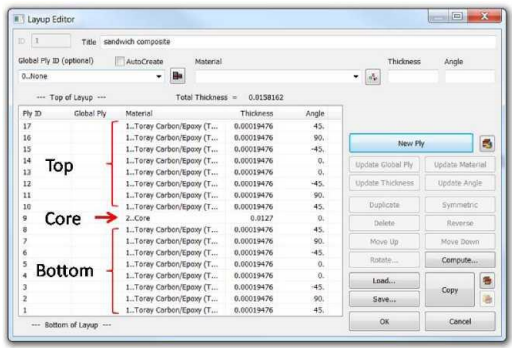
3. Использование классической теории пластин для моделирования сэндвич-композитов. Эта модель требует для реализации некоторого ручного вычисления, и поэтому сложна по сравнению с двумерной моделью композита. За свойства такой модели в Nastran отвечает функция PSHELL. В описанном выше методе 1, Nastran преобразует свойство PCOMP в эквивалентное свойство PSHELL. Таким образом, методы 1 и 2 должны давать схожие результаты, если все свойства точно определены. Чтобы избежать путаницы, метод 1 предпочтительнее метода 2, поскольку оба они одинаковы в том, как Nastran интерпретирует свойства. Кроме того, Femap имеет средства для задания сэндвич-композита с использованием метода PSHELL. Можно делать ручные вычисления и сравнивать их значения с вычисленным значением Femap, как показано ниже. Это средство для сэндвич-композитов доступно с помощью Custom tools, HoneycombPSHELL, Honeycomb PSHELL Property:

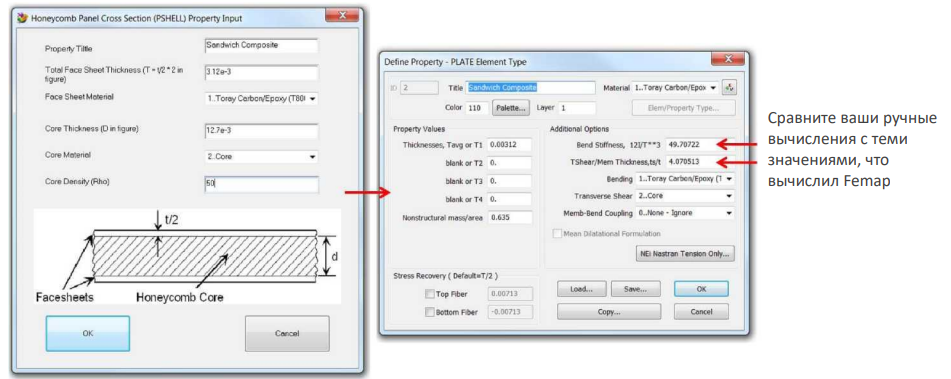
ТЕОРИИ РАЗРУШЕНИЯ КОМПОЗИТОВ В FEMAP

Введение

Поведение композитов является сложным из-за разнородности свойств, по сравнению с изотропными материалами. Понимание поведения композитов в условиях механической нагрузки, температуры и других факторов окружающей среды представляет собой серьезную проблему. Влияние условий эксплуатации на композитные конструкции может варьироваться от незначительной потери жесткости на микроуровне до катастрофического разрушения всей конструкции. Микроструктура композита развивается разными путями, прежде чем выявляется заметная деградация свойств. Типичные формы микромеханических сбоев включают разрушение волокна, растрескивание матрицы, разрыхление волокон /матрицы и т.д. Такие факторы, как микроразрушения (обычно в матрице), неизбежны и могут быть присущи изготовленной композитной детали. Микроразрушения могут быть результатом обработки композитов при высоких температурах (циклотверждения) из-за различий коэффициентов теплового расширения между компонентами (волокном, матрицей). Другие формы разрушения свойств композитного материала могут быть результатом гидротермальной нагрузки и окисления.

В этом разделе мы рассмотрим разрушение на уровне слоев, а не микромеханическое разрушение. Было разработано несколько теорий разрушения композитов. Теории разрушения, которые доступны в Femap, рассмотрим ниже. Некоторые из этих моделей разрушения (теория максимального напряжения, теория предельной деформации) основаны на чистом сравнении наблюдаемых напряжений/деформаций в композите с их соответствующими допускаемыми значениями. Другие модели, такие как теория Хилла, теория Цая-Ву и теория Хоффмана, рассматривают взаимодействие продольных/поперечных (трансверсальных) напряжений/деформаций для прогнозирования разрушения. Хотя теории разрушения могут быть удобными для проверки критериев разрушения и принятия решения о разрушении композита,важно понять распределение напряжений в модели, распределение межслоевых напряжений и их влияние на расслаивание, матрицы ABD (матрицы, связывающей деформации в плоскости композита с изгибными деформациями) и т.д.

Теория Хилла (HILL'S)

Теория разрушения Хилла применима к ортотропным материалам, которые имеют одинаковую прочность при растяжении и сжатии, т.е. xt = xc и yt = y. Критерий разрушения (FI - Failure Index) вычисляется по формуле:

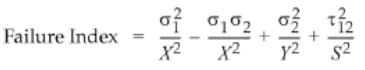
X – допускаемое напряжение по направлению 1

Y – допускаемое напряжение по направлению 2

S – допускаемое напряжение среза

Xt – допускаемое напряжение растяжения по направлению 1

Xc – допускаемое напряжение сжатия по направлению 1

Yt – допускаемое напряжение растяжения по направлению 2

Yc – допускаемое напряжение сжатия по направлению 2

X = Xt если s1 > 0 или X = Xc если s1 <0 и Y = Yt если s2 > 0 или Y = Yc если s2 <0. Для члена s1s2/X2, X = Xt если s1s2 >0 или X = Xc если s1s2 < 0.

Коэффициент прочности (SR) вычисляется как:

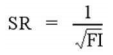
Теория Хоффмана (HOFFMAN'S)

В теории Хоффмана для ортотропной пластинки в обобщенном плоском напряженном состоянии с различной прочностью при сжатии и растяжении поверхность разрушения записывается так:

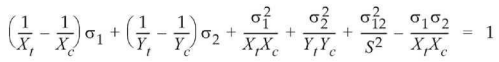
Критерий разрушения получается оценкой левой части приведенного выше уравнения.

Теория Цая-Ву (TSAI-WU)

Теория прочности для анизотропных материалов, предложенная Цаем и Ву, приведенная к случаю ортотропной пластинки в общем плоско-напряженном состоянии с различной прочностью на сжатие и растяжение:

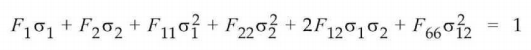
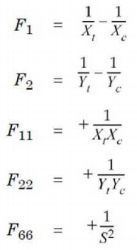
• Критерий разрушения получается оценкой левой части приведенного выше уравнения.
• F12 (коэффициент взаимодействия Цая-Ву) должен быть определен экспериментально. В Siemens Femap по умолчанию он устанавливается равным нулю.

Теория максимальных деформаций

• Критерий максимальной деформации не имеет коэффициентов взаимодействия, он вычисляется как:

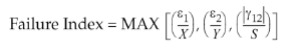
• X, Y, и S – это допускаемые деформации в продольном, поперечном направлении и сдвига, соответственно.
• Критерий разрушения для теории максимальных напряжения (доступный при моделировании трехмерного композита) можно вывести аналогично теории максимальной деформации.

Теория начала разрушения

Onset failure theory - Теория начала разрушения, или Strain Invariant Failure Theory (SIFT) - Теория разрушения на основе инвариантных деформаций, широко используется в аэрокосмической промышленности. Краткий обзор этого критерия разрушения приводится в конце статьи.

ПРИМЕР №4. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ МНОГОСЛОЙНЫХ КОМПОЗИТОВ ПРИ РАЗРУШЕНИИ

В этом примере будем использовать двумерную модель из КМ примера 1. Все процедуры моделирования, которые мы выполнили для нее, будут дополнены заданием предельных напряжений для пластинки и критериев разрушения. Цель состоит в том, чтобы изучить разрушение в многослойных композитах, а также исследовать выходные векторы, которые могут быть удобны при визуализации разрушения на уровне слоя и на уровне всего пакета.

Создание свойства материала

Укажите коэффициент взаимодействия Цая-Ву,если Вы используете критерий разрушения Цая-Ву:

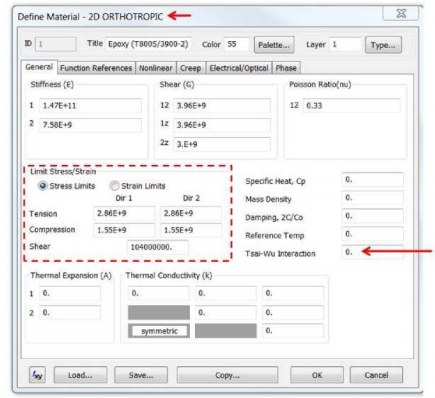
Задание свойств композита

Укладка пакета композита такая же, как в примере 1. Свойства определяется аналогичным образом. Кроме этого, мы выбираем теорию разрушения для расчета критериев разрушения на уровне слоя и для всего пакета. В этом примере мы будем использовать критерий разрушения Хоффмана. Допускаемое значение сдвига в связующем (ВondShr Allow) задается для прогнозирования разрушения связи между слоями. Если вас не интересует межслоевое разрушение, значение этого коэффициента можно оставить по умолчанию равным 0.

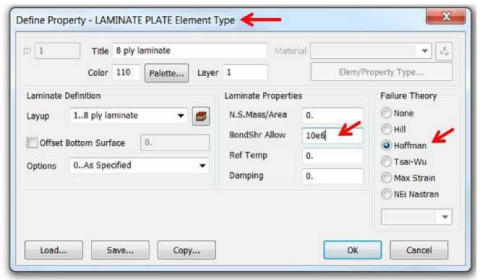
Задание направления материала следует выполнить так же как в примере 1.

Результаты

В этом примере нас в основном интересует изучение критериев разрушения и оценка пакета и отдельных слоев композита. К пластине прикладывается одноосная растягивающая нагрузка 50 кН. На рисунке ниже показаны контурные линии для критерия разрушения ламината, к которому можно получить доступ из выходного вектора –“6060 ...Laminate Max Failure Index”. Этот выходной вектор содержит общий критерий разрушения ламината. Значения уровня больше или равного 1.0 означает разрушение. Основываясь на этой информации, можно предположить, что есть один или несколько слоев, в которых происходит разрушение.

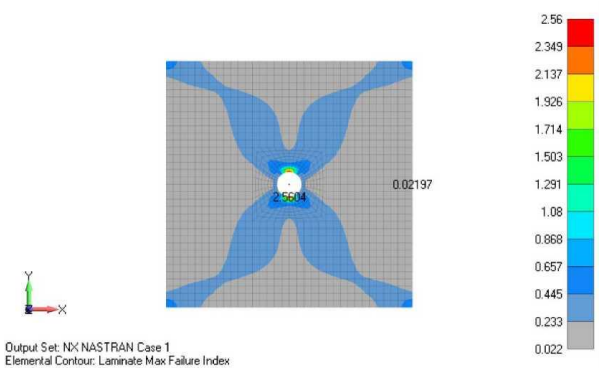
Затем мы можем проверить выходной вектор критерия разрушения по принципу «слой за слоем», чтобы найти слой, в котором происходит разрушение. Мы можем отобразить выходной вектор «Lam Ply Fib Fail Index» для конкретного слоя, а затем использовать опцию инструмента Custom Tools, PostProcessing, «Laminate Next Ply» или «Laminate Prev Ply» и проверить критерии разрушения. В меню Custom Tools, PostProcessing, у Femap есть макрос API для формирования вектора "Laminate EnvelopeFailure Indices" (Огибающие критериев разрушения ламината). В настоящее время эта функция API генерирует тот же выходной вектор, что и «6060 .. Laminate Max Failure Index». Однако, этот API может быть изменен пользователем для получения огибающей других выходных векторов, например, критериев разрушения связующего.

Если вы хотите вместо этого использовать ручной выбор выходных векторов для получения вектора огибающей, Вы можете использовать команду Model, Output, Process:

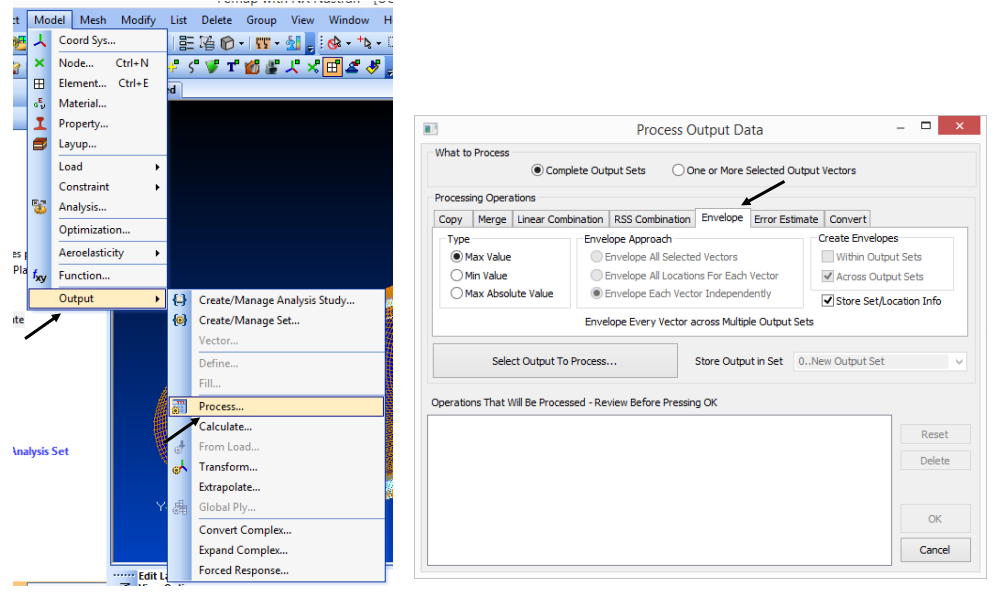
Ниже приведен пример получения огибающей наибольших главных напряжений всех слоев. Эту процедуру можно использовать для получения огибающей любого выходного вектора. Если в результате анализа получается только один выходной набор, мы можем получать огибающую выходных векторов из этого выходного набора. Однако, если у нас есть несколько выходных наборов, нам нужно выбрать один или несколько выходных наборов, для выходных векторов которых мы хотели бы получить огибающую.

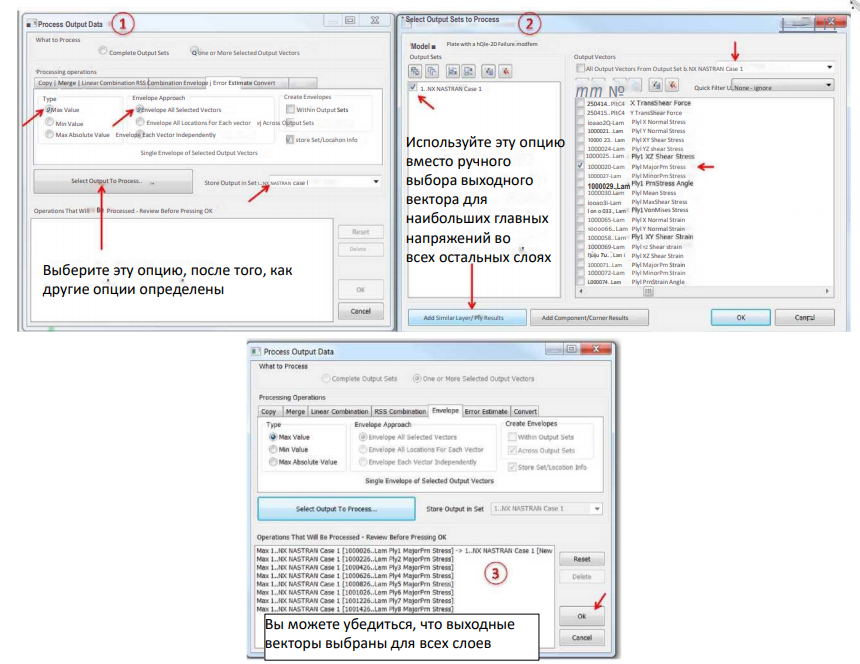
Это создаст новые выходные векторы, как показано ниже:

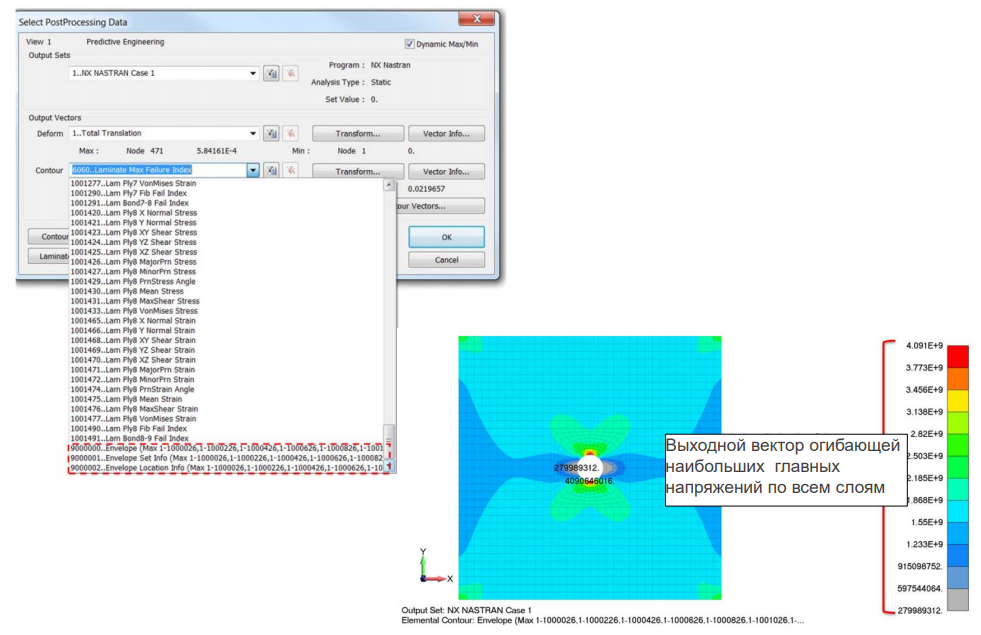
Попутно создаются другие выходные векторы, которые позволяют найти информацию о расположении (слоя и элемента), в котором действует максимальное наибольшее главное напряжение. Например, из приведенного выше рисунка мы можем видеть расположение элемента с максимальным наибольшим главным напряжением. Однако мы не знаем соответствующий слой, в котором действует это максимальное значение. Во вновь созданном выходном векторе «Location Envelope Info» будет эта информация. В окне команды View Options можно изменить значение опции Сontour/Сriteria Style, чтобы отображать только максимальное значение, минимальное значение или оба. Поскольку нас интересует только максимальное значение, нажмем горячую клавишу F6 (View Options), Postprocessing, Contour/CriteriaStyle, Max Only. Из заливки ниже видно, что максимальное значение наибольшего главного напряжения наблюдается в слое 4.

Дополнительные источники:

• Chapter 24: Laminates, NX Nastran User’s Guide2.
• "PCOMP and PCOMPS" in NX Nastran Quick Reference Guide3.
• Chapter 6: Element Reference – "Laminate Element and Solid Laminate Element" Femap User Guide.
• I. M. Daniel and O. Ishai, “Engineering Mechanics of Composite Materials, 2nd Edition", 2005.5.
• R. M. Jones, “Mechanics of Composite Materials, 2nd Edition", 1998.6.
• B. D. Agarwal, L. J. Broutman, and K. Chandrashekhara, “Analysis andPerformance of Fiber Composites, 3rd Edition", 2006.