Ранее в марте этого года мы опубликовали справочное руководство, посвященное некоторым недочетам, относящимся к анализу работы композитных деталей при потере продольной устойчивости в NX Nastran. В связи с тем, что несколько вопросов остались без ответа, а также из-за отзывов на исходную статью, стоит обновить наши выводы и прояснить некоторые неподтверждённые результаты. Предполагается, что читатель уже ознакомился с первой статьей, которую можно найти здесь. В дальнейшем мы приведем обновленные рекомендации о том, когда и каким образом можно применять офсеты на 2D-элементах, а также о том, как трактовать появление коротковолновых изгибов на панелях с наполнителем.
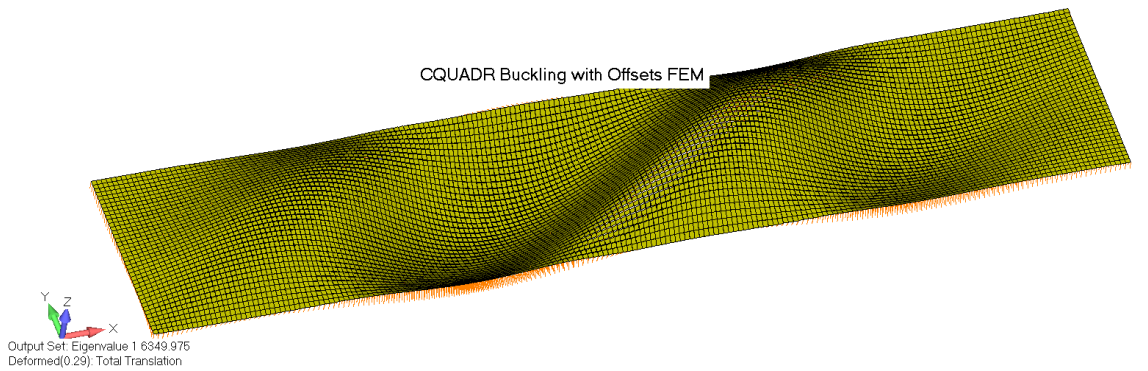
1.0 Потеря устойчивости с офсетами: задание на элементах или в свойствах
Один из вопросов, возникавших из полученных результатов исходного материала, заключался в следующем: “Как вы прикладывали офсеты? В свойствах или при построении элемента?” Оказывается, этот вопрос играет большую роль, хотя на этапе создания поверхностей пользователь NASTRAN может подумать: “А почему это должно иметь значение? Офсет не должен отличаться от способа задания – в свойствах элемента или при построении сетки”. Чтобы прояснить это обстоятельство для 6 тестовых образцов из первой статьи были использованы элементы CQUAD4/R/8 и свойства PSHELLметаллической пластины толщиной 0.05 дюйм. Единственным способом наложить офсеты на элементы, используя свойства PSHELL, является задание офсета в карте элемента.
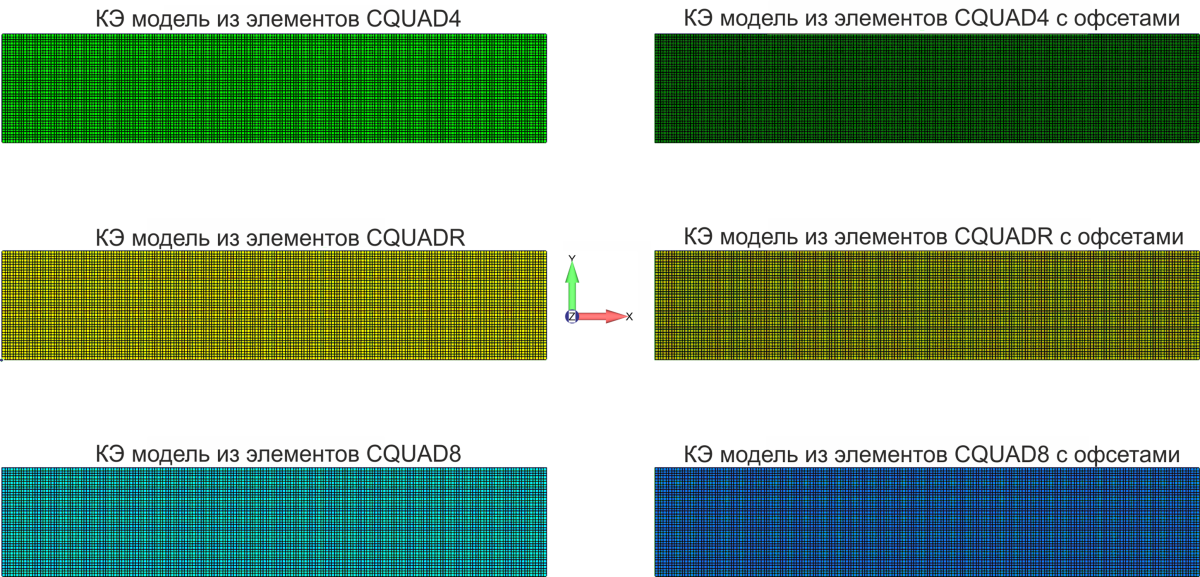
Те же 6 образцов были модифицированы для того, чтобы использовать свойства слоистого материалаPCOMP, содержащего 1 слой из того же алюминиевого материала с толщиной слоя 0.05дюйм (толщина в свойствах PSHELL исходных шести пластин). После модификации образцов для использования свойств PCOMP, в отличие от образцов со свойствами PSHELL, образцы с правой стороны также можно откорректировать, чтобы перевести офсет в карту свойств, вместо карты элемента. Затем повторно были проведены 3 отдельных реперных теста, результаты этих тестов можно увидеть в таблице 1.
Таблица 1: Результаты реперных тестов на потерю устойчивости для элементов со свойствами PCOMP и офсетами
Из этих результатов проясняются два обстоятельства. Первое – это очередное подтверждение того, что элементы CQUAD8 по-прежнему непригодны для использования, поскольку они не могут достоверно зафиксировать правильный характер изменения потери продольной устойчивости в реперных тестах со свободным опиранием при действии сдвигающей нагрузки. Если кому интересно, это исследование выполнено с использованием Simcenter Nastran 2019.1 (развитие версии NX Nastran 12.2). Вторая более информативная деталь заключается в том, что когда офсеты задаются в карте свойств PCOMP, а не в карте элемента, результаты, полученные от элементов CQUAD4 и CQUADR, довольно похожи. Так почему же так важно, где задавать офсеты?
Это, скорее всего, связано с классической теорией многослойных оболочек. Чтобы вычислить матрицу жесткости ABD для слоистого композиционного материала, интегрируют компоненты жесткости для каждого слоя в укладке, часто устанавливая пределы интегрирования от -H/2 до H/2, где H – полная толщина слоистого композита. Чтобы получить матрицу ABD слоистого композита с офсетом можно просто подобрать пределы интегрирования так, чтобы принять во внимание этот офсет. Например, для слоистого композита офсет в сторону к его нижней поверхности будет иметь значения пределов интегрирования от 0 до H. Поскольку такая процедура автоматически встроена в структуру картыPCOMP, смещения обрабатываются в целом незаметно для пользователя, выдавая жесткость элемента, который ссылается на данную карту. Хотя это достаточно хорошо описано в документации NASTRAN, кажется, что будто при задании офсета в карте элемента, используются мембранная и изгибная жесткости из свойства PSHELL,и которые преобразуются для учета офсета в рамках специальной процедуры. Поскольку эта процедура выполняется в ходе отдельных вычислений возможно, что либо она не выполняется до конца для геометрической матрицы жесткости элемента в линейном анализе потери устойчивости, либо приложенные к узлам нагрузки не переводятся обратно на среднюю плоскость, либо комбинация этих двух вариантов.
В конце предыдущего руководства на основе полученных результатов были сделаны противоречивые выводы: CQUAD4 элементы должным образом не учитывают офсеты, при этом элементы CQUADR неестественно податливы при поперечном сдвиге. Эти обновленные результаты показывают, что до тех пор, пока пользователь задает офсеты только в карте PCOMP, а не в карте элемента, применение элементов CQUAD4 является наиболее правильным методом моделирования композитных конструкций, поскольку при нем одновременно и корректно обрабатываются офсеты, и он имеет достоверную жесткость на поперечный сдвиг.
2.0 Коротковолновые изгибы
Несмотря на желание прекратить анализ этого вопроса в предыдущей статье, мы получили несколько комментариев, утверждающих, что коротковолновое коробление, которое мы наблюдали на моделях из слоистого композита, в действительности было поперечным обжатием. Мы не можем точно объяснить, почему оно проявляется при численном расчете, хотя в предыдущей статье делалось предположение о некоторых возможных причинах. Мы хотели бы безоговорочно опровергнуть представление, что эти изгибы вообще имеют какое-либо физическое значение.
2.1.1. Теоретическое исследование коротковолновых изгибов
В разделе 7.3 Теоретического руководства (Theoretical Guide) NX Nastran (стр. 323 в pdf-файле, который поставляется с Simcenter NASTRAN 2019.1) подробно описывается, как геометрическая (используется дифференциальная) матрица жесткости формулируется для любого 2D элемента плоского напряженного состояния. Прежде чем рассмотреть их получение, мы хотели бы разобрать немного более простой пример. Рассмотрим консольную балку с жесткостью на изгиб EI и жесткостью на поперечный сдвиг GAKs:

Полная потенциальная энергия на единицу длины балки равна:
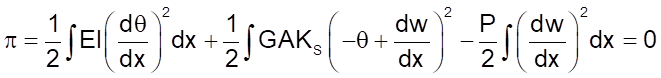
где
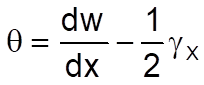
и 𝛾𝑦 – деформация сдвига балки. Обычно деформация сдвига для балок (и пластин) мала, поэтому этим членом можно пренебречь. Для таких конструкций, как короткие балки или панели с наполнителем, деформация сдвига становится довольно существенной, к тому же как раз и проявляются коротковолновые изгибы. Предположим, что рассматриваемая балка представляет собой сэндвич-балку с наполнителем, который моделирует работающую на срез перегородку, и с двумя слоистыми композитными пластинами, которые моделируют внешнюю облицовку.
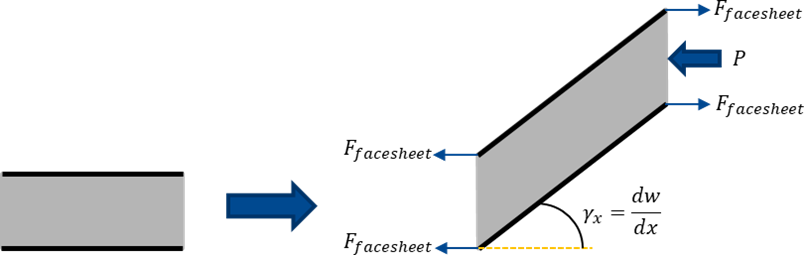
С учетом вышеупомянутой завышенной деформации сдвига нетрудно увидеть, что по мере того, как возрастает деформация сдвига, в той же степени увеличивается и длина балки. Поскольку облицовочные листы как правило жесткие, вместо того чтобы резко увеличиваться в длину, как это делает наполнитель, они создают большую нагрузку в плоскости. Эта нагрузка затем служит для некоторого восстановления возмущающей силы, которая возникает, когда все сечение целиком сжато, поэтому полная потенциальная энергия балки из уравнения 1 в таком случае приобретает вид:
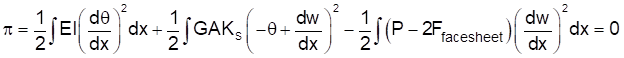
где
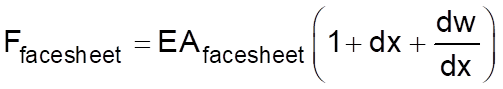
Так что это значит? В действительности при сдвиге панелей с наполнителем облицовочные листы создают восстанавливающее растягивающее усилие в плоскости, которое противодействует критической нагрузке потери устойчивости конструкции, предотвращая формирование чисто сдвигового характера потери устойчивости. Плоские элементы, такие как элементы CQUAD, не имеют степеней свободы для моделирования процесса образования этого растяжения в плоскости, и, соответственно, панели с наполнителем, смоделированные элементами CQUAD/CTRIA, подвержены возникновению полностью фиктивного коротковолнового изгиба, который обусловлен доминирующим действием сдвиговой нагрузки.
Интересно, что в Теоретическом руководстве (Theoretical Guide) NASTRAN предлагается для такой пластины деформацию сдвига не учитывать. Теоретически этого можно достичь, задав жесткость наполнителя на поперечный сдвиг бесконечной (или очень большой), чтобы устранить его податливость. Тогда возникает интересный вопрос, поскольку подразумевается, что жесткость на поперечный сдвиг не имеет большого значения в момент, когда пластина будет терять устойчивость.
2.1.1. Настройка тестовой модели
Для дальнейшего изучения этих концепций было создано четыре тестовых образца, чтобы смоделировать конструкции с малой жесткостью на поперечный сдвиг.

Образцы имитируют панели с наполнителем, укладка слоев которых имеет вид: [0/452/0/0.125” наполнитель/0/452/0].Светлые (1) и темные (3) оранжевые образцы смоделированы только с использованием элементов CQUAD4 и свойств PCOMP. Светлый (2) и темный (4)зеленые образцы смоделированы с использованием элементов CQUAD4 для облицовочных листов ([0/452/0]) и 4 элементов CHEXA, протянутых на толщину наполнителя. Чтобы различать эти два метода моделирования мы назовем оранжевые образцы образцами2D, а зеленые образцы – 2.5D. Ниже представлено увеличенное изображение одного из образцов 2.5D.
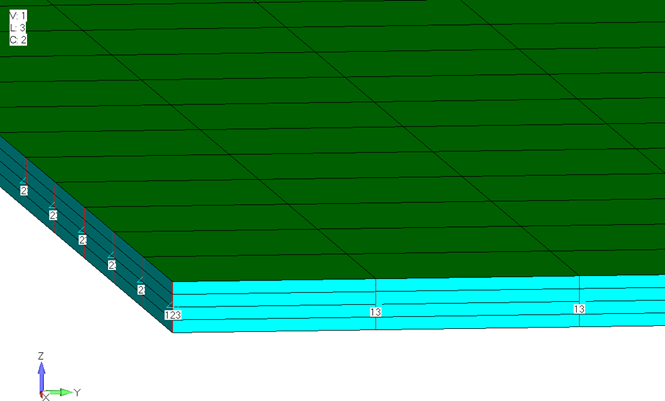
Можно заметить красные линии, которые идут по толщине этого образца. Это элементыRBE2, которые обеспечивают совместное движение облицовочных листов на границах пластин и служат в качестве удобного места для нагружения и закрепления сэндвич-панели.
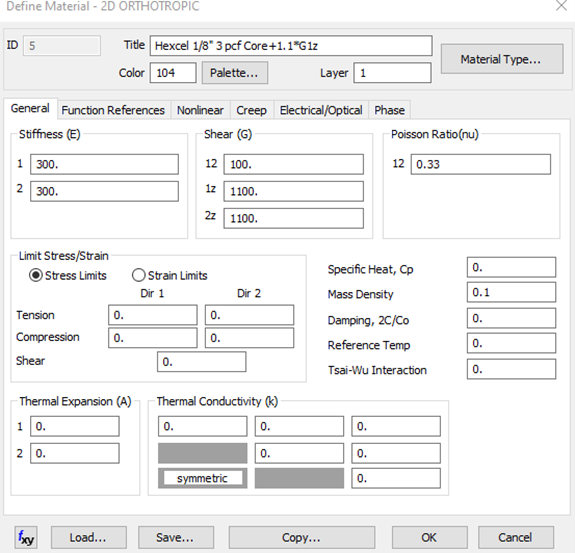
На следующих рисунках представлены свойства материалов, использованных при создании этих образцов:
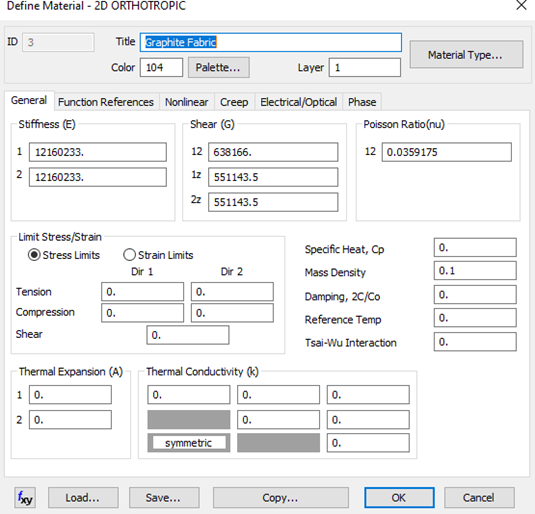
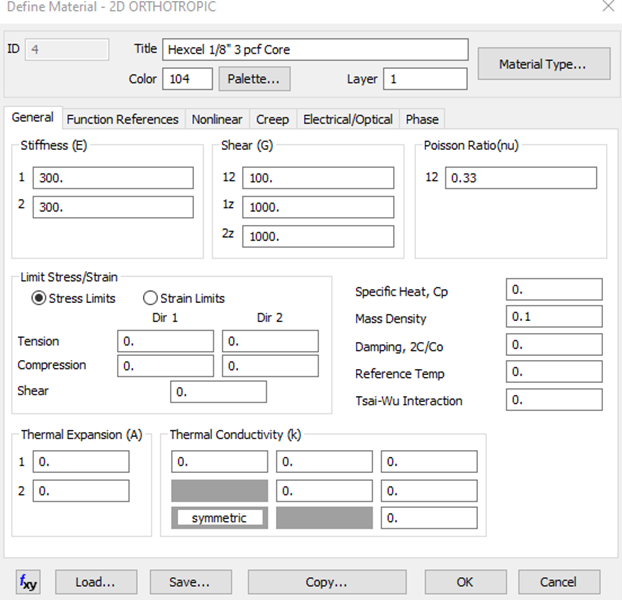
Разница между светлыми образцами (1,2) и темными образцами (3,4) заключается в том, что в более темных образцах компоненты G1z/2z наполнителя имею значения на 10% больше; это условие будет использоваться в дальнейшем для анализа степени чувствительности.
2.1.1. Задача Эйлера Бернулли
Для того, чтобы провести беглый тест анализ модели 2.5D, образцы 1 и 3 были закреплены в направлениях 2 и 3 (y и z) вдоль обеих коротких кромок, а также закреплены в направлении 1 (x) в двух верхних узлах, чтобы не допустить перемещение твердого тела:

Чтобы осуществить подготовку для нелинейного анализа, нагрузка прикладывалась к крайней правой кромке в виде вынужденного перемещения
0.0015295 дюйм в направлении -y, которое было итеративно отобрано для получения единичного собственного значения.
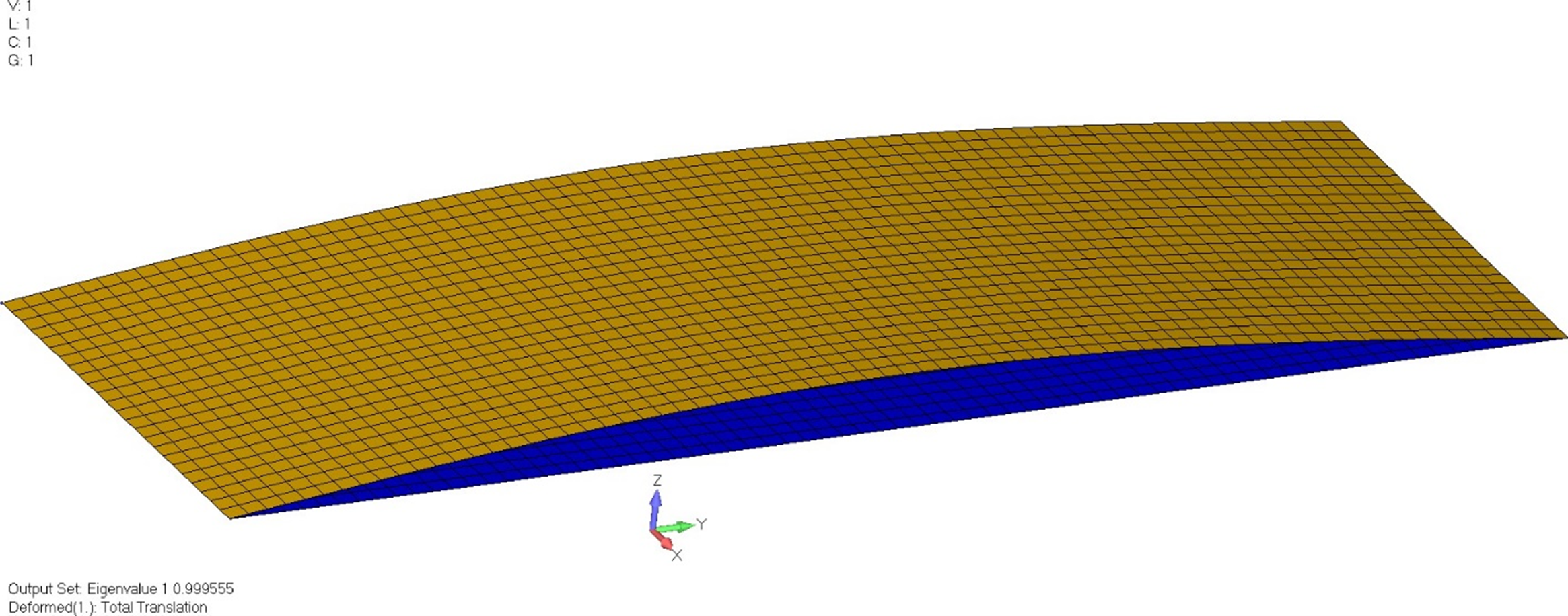
Образец (1) потерял устойчивость при собственном значении 0.99955 (~ 1), а образец (2) потерял устойчивость при собственном значении 1.02694, поэтому, хотя величины и не одинаковые, можно считать, они достаточно близки, особенно с учетом того, что формы колебаний в обоих случаях хорошо согласуются.
2.1.2. Задача об одноосной потере устойчивости при шарнирном опирании
Как правило коротковолновые изгибы появляются только в тех случаях, когда пластина закреплена со всех сторон, как например, в случае шарнирным опиранием. Вследствие чего образцы1 и 2 были закреплены в направлениях 2 и 3 (y и z) по обеим коротким кромкам, закреплены в направлениях 1 и 3 (x и z) по нижней кромке и в направлении 3 по верхней кромке:

Нагрузка была приложена в виде вынужденного перемещения 0.012893 в направлении -y. Как и ожидалось, первые 393 формы потери устойчивости на первый взгляд представляют собой случайные вариации коротковолновых изгибов с первым собственным значением~0.999902, постепенно увеличивающимся, по крайней мере, до 1.249227. На рисунках с 12 по 14 показаны примеры таких форм колебаний.
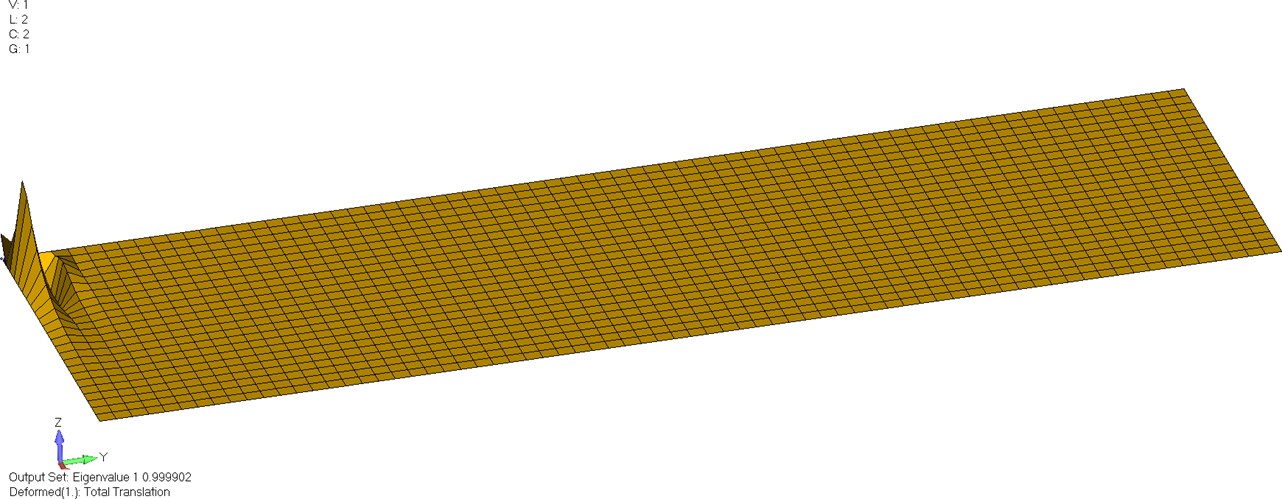


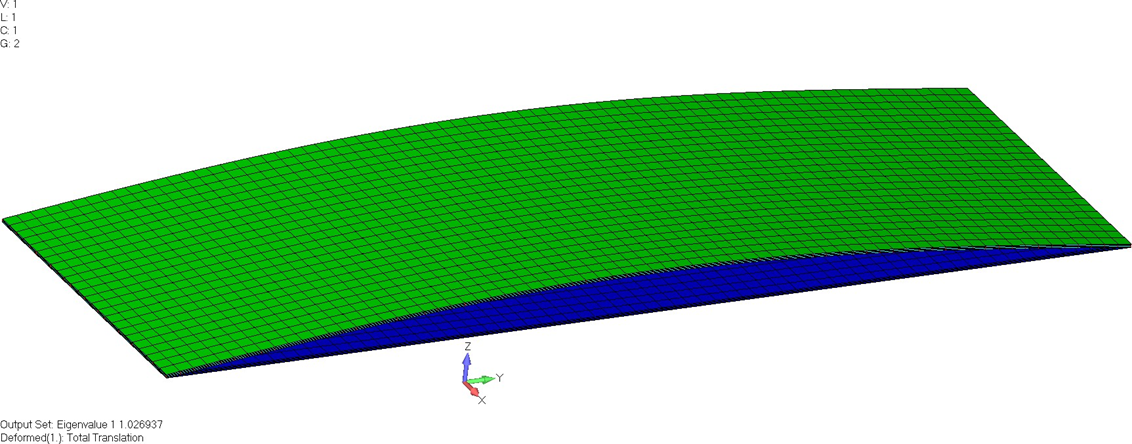
В то же время пара первого собственного значения и формы колебаний, полученная на модели 2.5D, дает форму колебаний, которая кажется правдоподобной, при собственном значении 1.200.

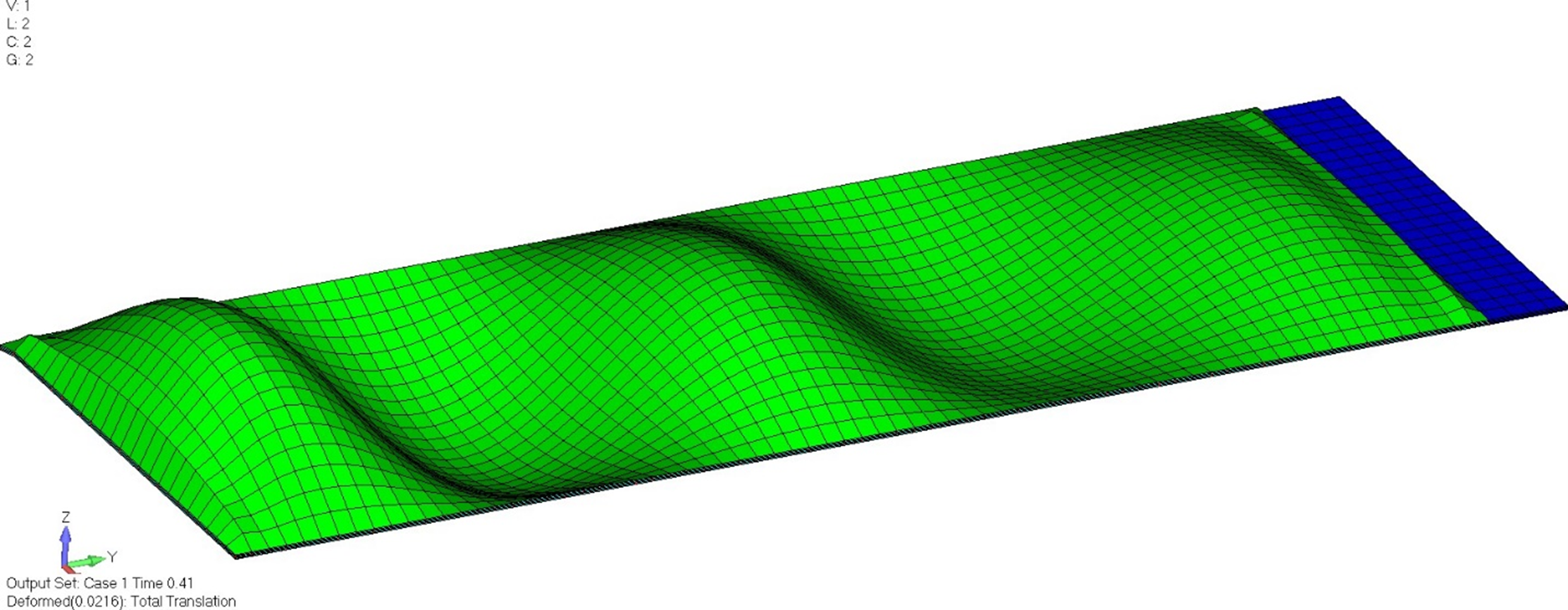
За счет моделирования наполнителя твердотельными элементами вертикальный прогиб (как например при деформации чистого сдвига) вызывает небольшое, но значительное удлинение облицовочных панелей, что приводит к образованию восстанавливающей растягивающей силы на этих панелях, рассмотренной в 2.1.1. Таким образом, при использовании 2.5D методики моделирования мы получаем точное решение задачи о потере устойчивости.
Важно отметить, что критическое собственное значение, полученное на 2.5D модели образца (2), никогда определяется на образце (1). Беспокоит то, что метод2D-моделирования не только создает множество фиктивных собственных значений, но также не позволяет достоверно определить правильное собственное значение/форму.
2.1.2.1. Подробнее о податливости наполнителя
Как было отмечено выше, ранее утверждалось что коротковолновые изгибы являются результатом коробления от сдвига или признаком того, что коробление от сдвига способно возникнуть. Используя актуальные характеристики материала, критическую нагрузку коробления сдвигом можно рассчитать как:
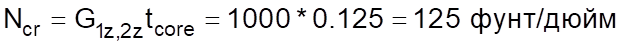
Нагрузка, при которой на образце (1) проявляются коротковолновые изгибы, составляет ~226 фунт/дюйм, что значительно больше фактической критической обжимающей нагрузки. На основании дальнейшего исследования мы думаем, коробление от сдвига является типом разрушения, который возможен только с сотовым наполнителем, так как он представляет собой потерю устойчивости стенок ячеек по всей толщине. Безусловно2.5D модель образца (2) не обладает достаточной точностью для моделирования таких форм потери устойчивости. С учетом этого кажется нелогичным предполагать, что тогда 2D CQUAD4 модель вообще будет способна передать такое поведение.
2.1.3. Задача о нелинейной одноосной потере устойчивости при свободном опирании
Хотя в этом нет необходимости, но было разумно также рассмотреть нелинейный расчет той же задачи из 2.1.4 в качестве способа сравнения, насколько сильно будет совпадать или отличаться нелинейное решение. Единственная разница между линейной и нелинейной моделями заключалась в том, что величина вынужденного перемещения была увеличена втрое для того, чтобы гарантировать, что потеря устойчивости возникает не от коэффициента масштаба нагрузки больше 1.0. Также к середине образцов была приложена небольшая возмущающая точечная сила.
Интересно отметить, образец (1) теряет устойчивость при собственном значении 1.035, что немного больше линейной оценки собственного значения в 0.99, хотя форма потери устойчивости проявляется в виде коротковолнового изгиба, к которому была приложена возмущающая критическая нагрузка.

Форма перемещений не согласуется с формами колебаний, вычисленными ранее в линейном анализе, и лишний раз показывает, насколько эти коротковолновые изгибы зависят от сетки. Это еще раз подчеркивает мнение о том, что изгибы действительно представляют собой неустойчивость численного решения.
Напротив, форма перемещений образца (2) довольно хорошо согласуется со спрогнозированными значениями линейного анализа, возникая при почти идентичном собственном значении 1.23, отклонение составляет 2.5%:
Чтобы взглянуть с другой стороны, выведем на график зависимость удельного вынужденного перемещения от силы реакции в качестве еще одного способа указания точек, где выгибается каждый образец. На рисунке ниже перемещение нормировано по критическому перемещению потери устойчивости для образца (2), а сила реакции нормирована по критической силе реакции потери устойчивости для образца (2).
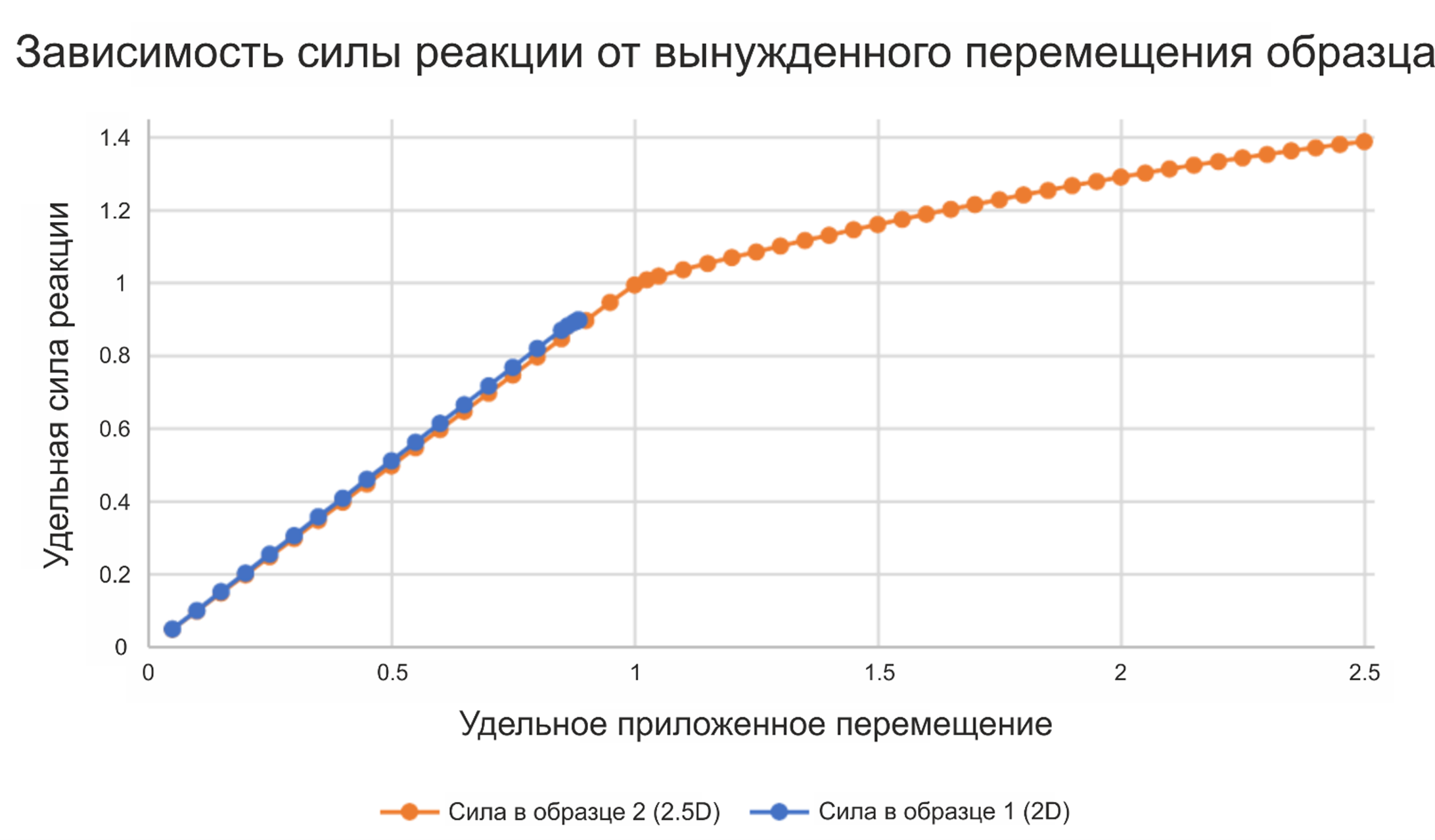
Нелинейное решение не может сойтись вскоре после достижения точки перегиба на образце (1),однако, для образца (2) перегиб удельной нагрузки (сигнализирующий о появлении выгиба) довольно хорошо различим.
2.1.4. Чувствительность потери устойчивости к жесткости наполнителя на поперечный сдвиг
В документации NASTRAN отмечалось, для того, чтобы решить проблему коротковолновых изгибов следует просто задать величину деформации сдвига равной нулю. Этого можно добиться, например, установив при моделировании очень большое значение жесткости наполнителя на поперечный сдвиг. Чтобы проверить справедливость этой гипотезы, мы можем просто провести исследование чувствительности из 2.1.2 посредством решения задачи о потере устойчивости со свободным опиранием из 2.1.4, используя наполнитель с увеличенной на 10% жесткостью на поперечный сдвиг.
Первое критическое собственное значение для образца (3) с использованием способа2D-моделирования дает почти идентичное собственное значение потери устойчивости1.15. Однако форма колебаний снова совершенно неадекватна и вместе с тем не физична.

В целом из этого мало что можно понять, кроме того, что некорректная методика моделирования в таком случае оказывается невосприимчивой к малым изменениям жесткости наполнителя на поперечный сдвиг.
Еще более интересны результаты для образца (4) с применением методики 2.5D моделирования. Собственное значение для образца (4) с 10%-ным увеличением жесткости наполнителя на поперечный сдвиг составляет 1.292, что на 7.6% больше, чем у образца (2) с аналогичной формой колебаний при потере устойчивости.

Это свидетельствует о том, что, как и следовало ожидать, жесткость наполнителя действительно оказывает некоторое неочевидное влияние на собственное значение потери устойчивости полой конструкции с малой жесткостью на поперечный сдвиг. Вопреки положениям документации NASTRAN, мы бы не согласились с тем, что можно просто игнорировать эффекты от влияния поперечного сдвига, задав соответствующую деформацию равной нулю.
3.0 Выводы
Полученные результаты этой статьи опровергают выводы предыдущей статьи о том, что у NASTRAN есть несколько неплохих вариантов анализа конструктивной устойчивости изделий из композитов при наличии офсетов. Фактически, решение по умолчанию с заданием офсетов в карте свойств слоистого композита и применение элементов CQUAD4 обуславливает точное решение. Это также означает, что нет необходимости прибегать к использованию элементов CQUADR, которые имеют некорректную формулировку жесткости на поперечный сдвиг, кроме случаев, когда решено задавать офсеты непосредственно в карте элемента.
В этой статье также достигается первоначальная цель предыдущей работы по объяснению некоторых обстоятельств основополагающей теории о том, почему коротковолновые изгибы в конструкциях с малой жесткостью на поперечный сдвиг (например, таких как панели с наполнителем) являются абсолютно нефизичными и, вероятно, имеют мало общего с другими типами разрушения, такие как поперечное обжатие и морщение листовой панели. Можно поспорить, что появление коротковолновых изгибов не лишено смысла, поскольку они указывают на то, что конструкция (скорее всего с податливым наполнителем) имеет малую жесткость на поперечный сдвиг. На что мы бы сказали, что расчетчик должен знать об использовании в конструкции податливого наполнителя, и поэтому при появлении коротковолновых изгибов каких-либо новых данных получено не будет.
Также высказывался противоположный аргумент, что, если допуск на поперечное обжатие при сдвиге положительный, можно игнорировать коротковолновые изгибы, однако в разделе 2.1.4 показано, что, применяя методику 2D-моделирования, можно вообще не заметить реальную потерю продольной устойчивости, которая полностью скрыта за нефизичными коротковолновыми изгибами.
И наконец, в этой статье представлены способы уменьшения роли коротковолновых изгибов при расчете продольной потери устойчивости на пластинчатой модели за счет использования твердотельных элементов для имитации наполнителя.





.svg)




























.jpg)
.jpg)



